Gracob: a novel graph-based constant-column biclustering method for mining growth phenotype data

Abstract

Motivation: Growth phenotype profiling of genome-wide gene-deletion strains over stress conditions can offer a clear picture that the essentiality of genes depends on environmental conditions. Systematically identifying groups of genes from such high-throughput data that share similar patterns of conditional essentiality and dispensability under various environmental conditions can elucidate how genetic interactions of the growth phenotype are regulated in response to the environment.

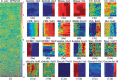
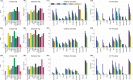
Results: We first demonstrate that detecting such 'co-fit' gene groups can be cast as a less well-studied problem in biclustering, i.e. constant-column biclustering. Despite significant advances in biclustering techniques, very few were designed for mining in growth phenotype data. Here, we propose Gracob, a novel, efficient graph-based method that casts and solves the constant-column biclustering problem as a maximal clique finding problem in a multipartite graph. We compared Gracob with a large collection of widely used biclustering methods that cover different types of algorithms designed to detect different types of biclusters. Gracob showed superior performance on finding co-fit genes over all the existing methods on both a variety of synthetic data sets with a wide range of settings, and three real growth phenotype datasets for E. coli, proteobacteria and yeast.

Availability and implementation: Our program is freely available for download at http://sfb.kaust.edu.sa/Pages/Software.aspx.

Contact: xin.gao@kaust.edu.sa.

Supplementary information: Supplementary data are available at Bioinformatics online.

Fig. 1

A minimalist example to illustrate environment-dependent genetic interactions. (a): Conditionally essential and dispensable genes. The circle, triangle and square symbols illustrate environmental inputs to the cell, for example input metabolites and ligands. Red, gray and black arrows denote active paths in wild type, inactive paths and active paths in each condition, respectively. The wild type grows normally under each condition, while the deletion of each gene has different effects on fitness under different conditions. $\Delta X$ denotes the strain of deleting gene X ($X\in \{A,B,C\}$). ‘GR’ and ‘NG’ stand for normal growth and no growth, respectively. (b): The corresponding growth phenotype data. Blue and red denote low and high fitness, respectively. The constant-column bicluster in the green box captures co-fit genes, A and B, which cannot be captured by any other constant biclusters

Fig. 2

Workflow of Gracob. (a): The data in each column are transformed using a cumulative distribution function, independently. (b): Data values in each column are sorted independently from other columns while keeping track of the original row indexes. (c): Nodes are created for each consecutive row subset such that the range of their values is at most δ (user defined value for how ‘constant’ each column of desired biclusters should be). A row subset can overlap with other row subsets but cannot be contained by others. (d): An edge is created between any pair of nodes if the nodes are from different columns and share at least r (user defined threshold for the smallest number of strains in desired biclusters) rows (i.e. strains). (e): Nodes with degree less than c (user defined threshold for the smallest number of conditions in desired biclusters) are deleted from the graph. (f): Each node is used to grow a clique with its connected nodes (orange circles) while thresholds, r and c, are repeatedly checked to detect future failures as early as possible. (g): Row and column index information from each clique is used to extract biclusters from the original data matrix

Fig. 3

Heatmap visualization of the E. coli growth phenotype data and the representative biclusters detected by the 11 methods. (1): The capped data matrix for the E. coli growth phenotype dataset with 3979 strains and 324 stress conditions. All the values bigger than 3.0 are capped as 3.0 and all the values smaller than -3.0 are capped as -3.0, for visualization purposes. (2)–(12): The representative biclusters detected by BicPAM, Bimax, CC, CPB, iBBiG, ISA, QUBIC, SAMBA, Spectral, xMOTIFs and Gracob, respectively. For each method, the predicted biclusters that have consistent patterns which appear many times in the results of this method are selected. For visualization purposes, rows and columns of each bicluster are organized by hierarchical clustering (Eisen et al., 1998). That is, genes with similar values are clustered on the Y-axis and conditions with similar values are clustered on the X-axis

Fig. 4

Performance comparison of the 11 methods on the E. coli, proteobacteria and yeast growth phenotype datasets. (1a)–(3a): The average column-wise standard deviation on the three datasets, respectively. (1b)–(3b): The average size of the returned biclusters on the three datasets, respectively. (1c)–(3c): The KEGG pathway-level precision under five significance levels on the three datasets, respectively. (1d)–(3d): The GO term-level precision under five significance levels on the three datasets, respectively