Identification of leader and self-organizing communities in complex networks

Abstract

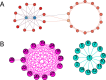
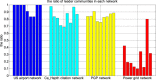
Community or module structure is a natural property of complex networks. Leader communities and self-organizing communities have been introduced recently to characterize networks and understand how communities arise in complex networks. However, identification of leader and self-organizing communities is technically challenging since no adequate quantification has been developed to properly separate the two types of communities. We introduced a new measure, called ratio of node degree variances, to distinguish leader communities from self-organizing communities, and developed a statistical model to quantitatively characterize the two types of communities. We experimentally studied the power and robustness of the new method on several real-world networks in combination of some of the existing community identification methods. Our results revealed that social networks and citation networks contain more leader communities whereas technological networks such as power grid network have more self-organizing communities. Moreover, our results also indicated that self-organizing communities tend to be smaller than leader communities. The results shed new lights on community formation and module structures in complex systems.

Figure 1

A network with both kinds of communities. (A) A leader community (left) and a self-organizing community that can be identified by the variance of node degree. The two communities have 14 nodes and an average node degree of 4. However, the degree variance of the leader community is 13.7 while the degree variance of the self-organizing community is 0. Here the degree of a node counters the edges within its community. (B) Another leader community (right) and a self-organizing community (left), each of which has 14 nodes. The leader community has an average node degree of 3.7 and a degree variance of 7.1. In contrast, the self-organizing community has a larger average node degree of 11.3 and a larger degree variance of 8.8. While the self-organizing community has a larger degree variance, it is not a leader community. Likewise, the leader community has a smaller degree variance than the self-organizing community, the former is a typical leader community.

Figure 2

Approximation of the expected degree variance with the average node degree in the ER network. This experimental analysis of the relationship between the expected variance of node degrees and the average degree was done on networks of four increasing sizes, N = 10, 100, 1000 and 10,000, with the average degrees of [0.5, 1, 1.5, …, 5, [2, 4, 6, …, 20], [3, 6, 9, …, 30], and [4, 8, 12, … 40], respectively. Each data point in the figure was averaged over 1,000 random problem instances.

Figure 3

VAR _real’s, VAR _rand’s and variance ratios of communities in real world networks with known community structures. Here VAR_real is the VAR of a community. VAR _rand’s in panel A are from simulation, averaged over M randomly generated ER networks with the same number of nodes N and average node degree, where M takes values of 500 and 1,000 and denoted as VAR_ER_500 and VAR_ER_1,000, respectively. As shown, VAR_ER_500 is almost the same as VAR_ER_1,000, suggesting that the approximation of VAR _rand via simulation is stable and efficient. Panel B shows the results from simulation and approximation VAR _rand = 〈k〉. Simulation with M = 1,000 is used for B(a) and B(b) and approximation for B(c) and B(d). The line in each diagram is the bound of VAR _rand = VAR _real. The ratios of p = VAR _real/VAR _rand are shown in panel C, where VAR _rand’s are from simulation with M = 1,000 as in B. The x-axes of the figures correspond to community sizies, which are ordered from small to large.

Figure 4

Variance ratios ρ of communities in (A) the US airport network, (B) Ca_Hepth citation network, (C) PGP network and (D) Power grid network that were discovered by 9 community-finding methods. Each figure for one of the four networks represents the result from one of the nine community-finding methods. For clarity, the x-axes correspond to community sizies, which are ordered from small to large. (A) In the US airport network, all of the communities, except four, have variance ratios ρ > 0, so that they were marked as leader communities. (B and C) In the Ca_Hepth citation network and the PGP networks, more leader communities were detected by the nine methods. (D) In the Power grid network, more self-organizing than leader communities were identified by eight of the nine algorithms, with Infomap as an exception.

Figure 5

The percentages of leader communities from nine community-finding methods on four real-world networks. Networks are color coded. For each network, nine bars corresponding to nine methods are in the same order as in Fig. 4.