A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex
- PMID: 28392071
- PMCID: PMC5498174
- DOI: 10.1016/j.neuron.2017.03.025
A Multiplexed, Heterogeneous, and Adaptive Code for Navigation in Medial Entorhinal Cortex
Abstract
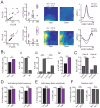
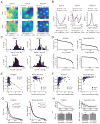
Medial entorhinal grid cells display strikingly symmetric spatial firing patterns. The clarity of these patterns motivated the use of specific activity pattern shapes to classify entorhinal cell types. While this approach successfully revealed cells that encode boundaries, head direction, and running speed, it left a majority of cells unclassified, and its pre-defined nature may have missed unconventional, yet important coding properties. Here, we apply an unbiased statistical approach to search for cells that encode navigationally relevant variables. This approach successfully classifies the majority of entorhinal cells and reveals unsuspected entorhinal coding principles. First, we find a high degree of mixed selectivity and heterogeneity in superficial entorhinal neurons. Second, we discover a dynamic and remarkably adaptive code for space that enables entorhinal cells to rapidly encode navigational information accurately at high running speeds. Combined, these observations advance our current understanding of the mechanistic origins and functional implications of the entorhinal code for navigation. VIDEO ABSTRACT.
Keywords: Multiplexed-coding; adaptive coding; computational models of spatial coding; encoding mode; entorhinal cortex; spatial navigation; tuning heterogeneity.
Copyright © 2017 Elsevier Inc. All rights reserved.
Figures



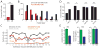

References
-
- Atkinson AC, Riani M, Cerioli A. The forward search: Theory and data analysis. Journal of the Korean Statistical Society. 2010;39:117–134.
-
- Bonnevie T, Dunn B, Fyhn M, Hafting T, Derdikman D, Kubie JL, Roudi Y, Moser EI, Moser MB. Grid cells require excitatory drive from the hippocampus. Nat Neurosci. 2013;16:309–317. - PubMed
-
- Brun VH, Leutgeb S, Wu HQ, Schwarcz R, Witter MP, Moser EI, Moser MB. Impaired spatial representation in CA1 after lesion of direct input from entorhinal cortex. Neuron. 2008;57:290–302. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

