Cooperativity and modularity in protein folding
- PMID: 28409080
- PMCID: PMC5221511
- DOI: 10.2142/biophysico.13.0_281
Cooperativity and modularity in protein folding
Abstract
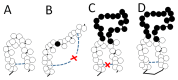
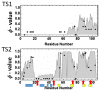
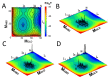
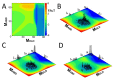
A simple statistical mechanical model proposed by Wako and Saitô has explained the aspects of protein folding surprisingly well. This model was systematically applied to multiple proteins by Muñoz and Eaton and has since been referred to as the Wako-Saitô-Muñoz-Eaton (WSME) model. The success of the WSME model in explaining the folding of many proteins has verified the hypothesis that the folding is dominated by native interactions, which makes the energy landscape globally biased toward native conformation. Using the WSME and other related models, Saitô emphasized the importance of the hierarchical pathway in protein folding; folding starts with the creation of contiguous segments having a native-like configuration and proceeds as growth and coalescence of these segments. The Φ-values calculated for barnase with the WSME model suggested that segments contributing to the folding nucleus are similar to the structural modules defined by the pattern of native atomic contacts. The WSME model was extended to explain folding of multi-domain proteins having a complex topology, which opened the way to comprehensively understanding the folding process of multi-domain proteins. The WSME model was also extended to describe allosteric transitions, indicating that the allosteric structural movement does not occur as a deterministic sequential change between two conformations but as a stochastic diffusive motion over the dynamically changing energy landscape. Statistical mechanical viewpoint on folding, as highlighted by the WSME model, has been renovated in the context of modern methods and ideas, and will continue to provide insights on equilibrium and dynamical features of proteins.
Keywords: WSME model; energy landscape; statistical mechanics.
Conflict of interest statement
Conflicts of Interest The authors declare no competing financial interest.
Figures




Similar articles
-
Thermodynamics and folding landscapes of large proteins from a statistical mechanical model.Curr Res Struct Biol. 2019 Oct 23;1:6-12. doi: 10.1016/j.crstbi.2019.10.002. eCollection 2019 Nov. Curr Res Struct Biol. 2019. PMID: 34235463 Free PMC article.
-
The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics.Molecules. 2022 Jul 12;27(14):4460. doi: 10.3390/molecules27144460. Molecules. 2022. PMID: 35889332 Free PMC article. Review.
-
Thermodynamics of protein folding using a modified Wako-Saitô-Muñoz-Eaton model.J Biol Phys. 2012 Sep;38(4):543-71. doi: 10.1007/s10867-012-9271-y. Epub 2012 Jun 21. J Biol Phys. 2012. PMID: 24615219 Free PMC article.
-
Quantitative prediction of protein folding behaviors from a simple statistical model.J Am Chem Soc. 2011 Apr 13;133(14):5372-9. doi: 10.1021/ja110884m. Epub 2011 Mar 18. J Am Chem Soc. 2011. PMID: 21417380
-
Ensemble-based methods for describing protein dynamics.Curr Opin Pharmacol. 2010 Dec;10(6):760-9. doi: 10.1016/j.coph.2010.09.014. Epub 2010 Oct 19. Curr Opin Pharmacol. 2010. PMID: 20965786 Free PMC article. Review.
Cited by
-
Thermodynamics and folding landscapes of large proteins from a statistical mechanical model.Curr Res Struct Biol. 2019 Oct 23;1:6-12. doi: 10.1016/j.crstbi.2019.10.002. eCollection 2019 Nov. Curr Res Struct Biol. 2019. PMID: 34235463 Free PMC article.
-
Memorial Issue for Professor Nobuhiko Saitô.Biophys Physicobiol. 2016 Nov 18;13:243. doi: 10.2142/biophysico.13.0_243. eCollection 2016. Biophys Physicobiol. 2016. PMID: 28409076 Free PMC article. No abstract available.
-
The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics.Molecules. 2022 Jul 12;27(14):4460. doi: 10.3390/molecules27144460. Molecules. 2022. PMID: 35889332 Free PMC article. Review.
-
Unified understanding of folding and binding mechanisms of globular and intrinsically disordered proteins.Biophys Rev. 2018 Apr;10(2):163-181. doi: 10.1007/s12551-017-0346-7. Epub 2018 Jan 6. Biophys Rev. 2018. PMID: 29307002 Free PMC article. Review.
-
Accurate prediction of protein folding mechanisms by simple structure-based statistical mechanical models.Nat Commun. 2023 Oct 19;14(1):6338. doi: 10.1038/s41467-023-41664-1. Nat Commun. 2023. PMID: 37857633 Free PMC article.
References
-
- Wako H, Saitô N. Statistical mechanical theory of the protein conformation. I. General considerations and the application to homopolymers. J Phys Soc Jpn. 1978;44:1931–1938.
-
- Wako H, Saitô N. Statistical mechanical theory of the protein conformation. II. Folding pathway for protein. J Phys Soc Jpn. 1978;44:1939–1945.
-
- Lifson S, Roig A. On the theory of helix-coil transition in polypeptides. J Chem Phys. 1961;34:1963–1974.
-
- Poland D, Scheraga HA. Phase transitions in one dimension and the helix-coil transition in polyamino acids. J Chem Phys. 1966;45:1456–1463. - PubMed
-
- Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 1995;21:167–195. - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
