Estimating optimal sparseness of developmental gene networks using a semi-quantitative model

Abstract

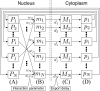
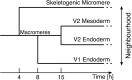
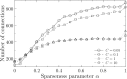
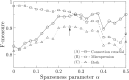
To estimate gene regulatory networks, it is important that we know the number of connections, or sparseness of the networks. It can be expected that the robustness to perturbations is one of the factors determining the sparseness. We reconstruct a semi-quantitative model of gene networks from gene expression data in embryonic development and detect the optimal sparseness against perturbations. The dense networks are robust to connection-removal perturbation, whereas the sparse networks are robust to misexpression perturbation. We show that there is an optimal sparseness that serves as a trade-off between these perturbations, in agreement with the optimal result of validation for testing data. These results suggest that the robustness to the two types of perturbations determines the sparseness of gene networks.

Fig 1. Model structure.

Boxes show variables: (A) binary protein, (B) mRNA, (C) binary mRNA, and (D) protein. Arrows imply biological processes: (A)→(B) transcription, (B)→(C) mRNA export, (C)→(D) translation, and (D)→(A) protein import.

Fig 2. Time course of cell differentiation in the model.

A signal can be transferred between only neighbouring domains.

Fig 3. Number of estimated connections as a function of sparseness parameter α.

We show the average number for each soft-margin parameter C in 1,000 optimal solutions. The other parameters are fixed at d = 2 [h], d_min = 0 [h], d_max = 2 [h], and θ = 1.

Fig 4. Accuracy for time-series data as a function of sparseness parameter α.

We show the average F-measure for each soft-margin parameter C in 1,000 optimal solutions. F-measure is calculated in the experimental data after 6 h. The other parameters are fixed at d = 2 [h], d_min = 0 [h], d_max = 2 [h], ϵ = 0.5, and θ = 1.

Fig 5. Estimated time series of mRNA expressions.

These time series are examples at α = 0.25 and C = 0.1, and we use the first optimal solution. Compared with the experimental data, each expression is classified into True Positive (TP), True Negative (TN), False Positive (FP), or False Negative (FN). The other parameters are fixed at d = 2 [h], d_min = 0 [h], d_max = 2 [h], ϵ = 0.5, and θ = 1.

Fig 6. Accuracy for gene perturbation data as a function of sparseness parameter α.

We show the average F-measure for each soft-margin parameter C in 1,000 optimal solutions. The optimal F-measure is observed at (α, C) = (0.25, 0.1) (indicated by an arrow). The other parameters are fixed at d = 2 [h], d_min = 0 [h], d_max = 2 [h], ϵ = 0.5, and θ = 1.

Fig 7. Robustness of perturbed networks as a function of sparseness parameter α.

As the robustness, we show the average F-measure in 1,000 optimal solutions. The types of perturbations are (A) connection-removal perturbation (n_c = 10), (B) misexpression perturbation (λ = 10, μ = 0.01), and (C) the addition of both perturbations. Optimal robustness in (C) is observed at α = 0.25 (indicated by an arrow). The other parameters are fixed at C = 0.1, d = 2 [h], d_min = 0 [h], d_max = 2 [h], ϵ = 0.5, and θ = 1.

Fig 8. Robustness of perturbed networks as a function of sparseness parameter α at various noise intensities (A) λ = 10, (B) λ = 20, and (C) λ = 30.

Both connection-removal and misexpression perturbations are applied to the estimated networks. As the robustness, we show the average F-measure for each number of connection removals n_c in 1,000 optimal solutions. The filled mark indicates the maximum value in each profile. The other parameters are fixed at μ = 0.01, C = 0.1, d = 2 [h], d_min = 0 [h], d_max = 2 [h], ϵ = 0.5, and θ = 1.