Nonreciprocal charge transport in noncentrosymmetric superconductors

Abstract

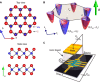
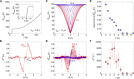
Lack of spatial inversion symmetry in crystals offers a rich variety of physical phenomena, such as ferroelectricity and nonlinear optical effects (for example, second harmonic generation). One such phenomenon is magnetochiral anisotropy, where the electrical resistance depends on the current direction under the external magnetic field. We demonstrate both experimentally and theoretically that this magnetochiral anisotropy is markedly enhanced by orders of magnitude once the materials enter into a superconducting state. To exemplify this enhancement, we study the magnetotransport properties of the two-dimensional noncentrosymmetric superconducting state induced by gating of MoS₂. These results indicate that electrons feel the noncentrosymmetric crystal potential much coherently and sensitively over the correlation length when they form Cooper pairs, and show open a new route to enhance the nonreciprocal response toward novel functionalities, including superconducting diodes.

Keywords: Ginzburg-Landay Theory; magnetochiral anisotropy; noncentrosymmetric superconductor; nonreciprocal response; paraconductivity.

Fig. 1. Schematic illustration of nonreciprocal transport in noncentrosymmetric bulk crystals.

(A) I-V curve in the normal state of a noncentrosymmetric crystal, whose nonreciprocal current is usually small. (The dashed line is the linear I-V relation.) Inset: Electron motion in the asymmetric potential, which represents the lack of inversion symmetry. (B) I-V curve in the resistive superconducting state, whose nonreciprocal current is much larger than that of the normal state below the critical current (I_c), whereas it remains unchanged at larger I. Inset: Enhanced nonreciprocity due to the coherence of Cooper pairs.

Fig. 2. Crystal and band structures of 2H-MoS₂ and experimental setup.

(A) Top and side views of a 2H-MoS₂ 2D crystal. In monolayers, spatial inversion symmetry is broken because the Mo and S sites are not equivalent, but the inversion symmetry is restored in 2H-type multilayers. (B) Schematic band structure of the conduction bottom of 2D MoS₂. The magnetic field is applied perpendicular to the plane. Owing to the combination of the spin-orbit interaction and Zeeman effect, the band asymmetry appears between the K and K′ = −K points. Their spin splittings are 2(Δ_SO + Δ_Z) and 2(Δ_SO − Δ_Z), respectively. (C) Schematic image of a MoS₂-EDLT. V_xx is a four-probe longitudinal voltage of the channel. Here, the channel direction was parallel to the zigzag edge (29).

Fig. 3. Magnetochiral anisotropy in ion-gated MoS₂.

(A) Temperature (T) dependence of sheet resistance R_sheet of a MoS₂-EDLT at a gate voltage V_G of 5.0 V. Inset: A close-up of the resistive transition. The T_c is 8.8 K as defined at the midpoint of the transition with sheet resistance R_sheet being 50% of the normal state. (B) Antisymmetrized sheet $({\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }},\text{red})$ and Hall $({\mathit{R}}_{\text{Hall}}^{2\mathrm{\omega }},\text{black})$ second harmonic magnetoresistance at 2 K. Compared to the signals of ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$, the value of ${\mathit{R}}_{\text{Hall}}^{2\mathrm{\omega }}$ is much smaller. (C) Magnetoresistance at 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, and 15K at I_DS of 17 μA. (D) Antisymmetrized second harmonic sheet magnetoresistance ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ at 2 to 10 K. (E) Maximum of the ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}$ as a function of temperature. (F) Temperature dependence of γ at the I_DS of 17 μA. The γ suddenly increases up to ~1200 T⁻¹ A⁻¹ around the superconducting transition. Error bars are estimated by the uncertainty of the R_sheet because of the broad peak of the ${\mathit{R}}_{\text{sheet}}^{2\mathrm{\omega }}\dot{}$