A unifying mathematical framework for experimental TCR-pMHC kinetic constants

Abstract

Receptor binding and triggering are central in Immunology as T cells activated through their T cell receptors (TCR) by protein antigens orchestrate immune responses. In order to understand receptor-ligand interactions, many groups working with different experimental techniques and assays have generated a vast body of knowledge during the last decades. However, in recent years a type of assays, referred to as two-dimensional or membrane-to-membrane, has questioned our current understanding of the role of different kinetic constants (for instance, on- versus off-rate constants) on TCR-ligand interaction and subsequent T cell activation. Here we present a general mathematical framework that provides a unifying umbrella to relate fundamental and effective (or experimentally determined) kinetic constants, as well as describe and compare state-of-the-art experimental methods. Our framework is able to predict the correlations between functional output, such as 1/EC₅₀, and effective kinetic constants for a range of different experimental assays (in two and three dimensions). Furthermore, our approach can be applied beyond Immunology, and serve as a "translation method" for the biochemical characterization of receptor-ligand interactions.

Figure 1. Correlation between T cell proliferation (potency), quantified through the value of 1/EC₅₀, and TCR-pMHC effective kinetic parameters in 3D and 2D.

(a–c) pMHC functional potency versus TCR-pMHC 3D kinetics estimated with the surface plasmon resonance assay. (d–f) pMHC functional potency versus TCR-pMHC 2D kinetics estimated with the adhesion frequency assay. The data for the top row was adapted from refs ,, and data for the bottom row is based on ref. . Symbols correspond to the following ovalbumin-derived peptides (altered peptide ligands or APLs): ★, OVA; ⚪, A2; ×, G4; , E1; , V-OVA; , R4.

Figure 2. Three steps of binding in three versus two dimensions.

Top row, binding in three dimensions: (A) 3D diffusion/encounter, (B) rotation/orientation, and (C) molecular binding. Bottom row, the three binding steps in two dimensions: (D) 2D (membrane) diffusion/encounter, (E) rotation/orientation, and (F) molecular binding. The vertical line separates dimensional dependent and independent processes. The fundamental kinetic constants corresponding to each step in 3D and 2D have been included: , for diffusion/encounter, e⁺, e⁻ for rotation/orientation and k⁺, k⁻ for binding and unbinding, respectively. The fundamental kinetic constants are defined in Table 1.

Figure 3. Summary of effective models. Species with angular brackets (〈.〉) denote effective meta-states.

These meta-states account for the lack of microscopic details in the given experimental assay. For each model, the first row shows the full model with green boxes that emphasize the implicit grouping behind a given experimental assay, and the second row describes the corresponding simplified or effective model.

Figure 4. Observed and expected trend lines between T cell functional output and effective (AF assay-derived) and fundamental kinetic constants for the set of peptides used in Fig. 1.

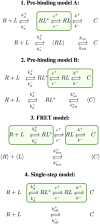
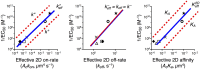
The blue solid lines correspond to the effective kinetic constants, , , and , as determined with the AF assay and the SS model. The red lines correspond to the fundamental binding constants (k⁺, k⁻ and K_A). A dashed red line indicates an uncertainty in the direction and magnitude of the shift corresponding to a given fundamental binding parameter, depending on whether is positive or negative and whether is relatively large or small. See details in Cases 1, 2 and 4.

Figure 5. Observed and expected trend lines between T cell functional output and effective kinetic constants, derived from the 2D FRET and AF assays, for the set of peptides used in Fig. 1.

The dark blue lines correspond to the effective kinetic constants , , and from the AF assay. The cyan lines are the predicted trend lines for the correlation between log(1/EC₅₀) and the logarithm of the effective parameters , , and from the 2D FRET assay, as inferred using the results in Cases 1 and 3 and further discussed in Case 4. Dashed vertical lines are drawn to help visualize the asymptotic limits of and . Their particular positions, as well as that of cyan lines, are for illustrative purposes.

Figure 6. Observed and expected trend lines between T cell functional output and effective kinetic constants, derived from the 3D FRET and SPR assays, for the set of peptides used in Fig. 1.

The dark blue lines correspond to the effective kinetic constants , , and from the SPR assay. The cyan lines are the predicted trend lines for the correlation between log(1/EC₅₀) and the logarithm of the effective parameters , , and from the 3D FRET assay, as inferred using the results in Case 5. Dashed vertical lines are drawn to help visualize the asymptotic limits of and . Their particular positions, as well as that of cyan lines, are for illustrative purposes.