When do correlations increase with firing rates in recurrent networks?

Abstract

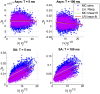
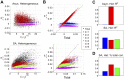
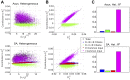
A central question in neuroscience is to understand how noisy firing patterns are used to transmit information. Because neural spiking is noisy, spiking patterns are often quantified via pairwise correlations, or the probability that two cells will spike coincidentally, above and beyond their baseline firing rate. One observation frequently made in experiments, is that correlations can increase systematically with firing rate. Theoretical studies have determined that stimulus-dependent correlations that increase with firing rate can have beneficial effects on information coding; however, we still have an incomplete understanding of what circuit mechanisms do, or do not, produce this correlation-firing rate relationship. Here, we studied the relationship between pairwise correlations and firing rates in recurrently coupled excitatory-inhibitory spiking networks with conductance-based synapses. We found that with stronger excitatory coupling, a positive relationship emerged between pairwise correlations and firing rates. To explain these findings, we used linear response theory to predict the full correlation matrix and to decompose correlations in terms of graph motifs. We then used this decomposition to explain why covariation of correlations with firing rate-a relationship previously explained in feedforward networks driven by correlated input-emerges in some recurrent networks but not in others. Furthermore, when correlations covary with firing rate, this relationship is reflected in low-rank structure in the correlation matrix.

Fig 1. Two firing regimes in heterogeneous networks.

Monte Carlo simulations illustrating two firing regimes we consider in this paper. (A) Raster plots from the asynchronous (Asyn) regime. (B) Raster plots from the strong asynchronous (SA) regime, showing occasional bursts of activity. (C) Power spectra in the asynchronous regime. (D) Power spectra in the strong asynchronous regime. (E) Firing rates in the asynchronous (top panel) and SA (bottom panel) regimes. In (A-B), cells are ordered by increasing threshold value. Power spectra (C-D) are normalized to their maximum value and expressed in decibels/Hz.

Fig 2. Correlation increases with firing rate in the strong asynchronous regime.

E-E correlation ρ_ij vs. geometric mean firing rate $\sqrt{{\nu }_i{\nu }_j}$, cell-by-cell comparison of Monte Carlo simulations (blue stars) and linear response (magenta circles), in a heterogeneous network. Left to right: time window T = 5 ms and 100 ms. Top row: asynchronous regime. Bottom row: strong asynchrony.

Fig 3. Pairwise correlations are built from graph motifs.

Contributions of different orders to prediction of E-E correlations with linear response theory. (A) Normalized contributions to pairwise correlation (${\tilde{\mathbf{R}}}_{ij}^k$) vs. geometric mean firing rate ($\sqrt{{\nu }_i{\nu }_j}$) for heterogeneous networks in the asynchronous (top panel) and strong asynchronous (bottom panel) regimes. (B) As in (A), but plotted vs. total predicted normalized correlation (${\tilde{\mathbf{C}}}_{ij}/\sqrt{{\tilde{\mathbf{C}}}_{ii}{\tilde{\mathbf{C}}}_{jj}}$). See main text for further discussion. (C) To quantify the relative importance of different motifs, we report the fraction of variance explained (R²) from linear regressions, in which we regressed total correlation (${\tilde{\mathbf{C}}}_{ij}/\sqrt{{\tilde{\mathbf{C}}}_{ii}{\tilde{\mathbf{C}}}_{jj}}$) against the contributions at each specific order (${\tilde{\mathbf{R}}}_{ij}^k$). As suggested by (B), second-order contributions (red) overwhelmingly determine total correlations in the asynchronous network (R² values for first- and third-order terms are shown, but barely visually distinguishable; R² values for higher orders are also small, within 0.08 up to k = 6). (D) Fraction of total correlation from each order, strong asynchronous regime.

Fig 4. Inhibitory common input is the dominant second-order motif in both asynchronous and strong asynchronous networks.

(A) Contributions of different 2nd-order motifs to prediction of E-E correlations in a heterogeneous network, in the asynchronous (top) and strong asynchronous (bottom) regimes. (B) As in (A), but plotted vs. total contribution from second-order motifs ${\tilde{\mathbf{R}}}^2$. In both panels, inhibitory common input (magenta) clusters near the unity line. (C) To quantify the relative importance of different motifs, we report the fraction of variance explained (R²) from linear regressions, in which we regressed the total contribution from second-order motifs (${\tilde{\mathbf{R}}}_{ij}^k$) against the contribution from specific motifs types.

Fig 5. Susceptibility to conductance fluctuations can explain correlation-firing rate relationships.

In (A-C): heterogeneous asynchronous (top) and heterogeneous strong asynchronous (bottom). (A) Correlation (ρ) from I common inputs vs. firing rate, segregated based on the number of common inhibitory inputs. (B) Estimated correlation susceptibility to fluctuations in inhibitory conductances vs. firing rate ($S_{ij}^{g_I}$). (C) Correlation susceptibility to fluctuations in inhibitory currents vs. firing rate ($S_{ij}^{\mu }$).

Fig 6. How firing rate diversity is achieved in a heterogeneous network will affect susceptibility.

Single-cell susceptibility function(s) for a conductance-based LIF neuron, as a function of firing rate ν. Successive approximations shown are: original single-cell susceptibility, $S_i^{\langle g_I\rangle }$ (Eq 4, blue stars); most parameters set to average value, ${\widehat{S}}_i^{\langle g_I\rangle }$ (Eq 7, red triangles); all parameters but θ_i set to average value, ${\widehat{\widehat{S}}}_i^{\langle g_I\rangle }$ (Eq 9, gold squares); and θ fixed, ${\widehat{S}}_{\theta =1}^{\langle g_I\rangle }$ (Eq 10, purple diamonds). (A) Asynchronous regime. (B) Strong asynchronous regime.

Fig 7. Susceptibility as a function of inhibitory conductance and threshold.

Single-cell susceptibility function for a conductance-based LIF neuron, as a function of mean inhibitory conductance 〈g_I〉 and threshold θ: ${\widehat{S}}^{\langle g_I\rangle }(\langle g_I\rangle ,\theta )$ (defined in Eq 7). Other parameters are set to the population average. Overlays show (〈g_I,i〉, θ_i) values of the actual cells in the network (red stars) and an alternative curve through the plane, (〈g_I〉, 1), along which comparable firing rate diversity can be observed (black squares). (A) Asynchronous regime. (B) Strong asynchronous regime.

Fig 8. Low-rank structure in correlation matrices.

Approximating correlation matrices for the heterogeneous networks as a diagonal plus rank-one. Neurons are ordered by firing rate (highest to lowest). In each column of (A-D), the asynchronous (top) and strong asynchronous (bottom) regimes are shown; T = 100 ms.(A) The shifted E-E correlation matrix, C_T − λI, for an appropriately chosen λ. (B) A rank-one approximation to C_T − λI. (C) True correlation coefficients vs. rank-one approximation, cell-by-cell. (D) Weight in the first singular vector, u₁ vs. geometric mean firing rate $\sqrt{{\nu }_i{\nu }_j}$.