Compressed sensing MRI via fast linearized preconditioned alternating direction method of multipliers

Abstract

Background: The challenge of reconstructing a sparse medical magnetic resonance image based on compressed sensing from undersampled k-space data has been investigated within recent years. As total variation (TV) performs well in preserving edge, one type of approach considers TV-regularization as a sparse structure to solve a convex optimization problem. Nevertheless, this convex optimization problem is both nonlinear and nonsmooth, and thus difficult to handle, especially for a large-scale problem. Therefore, it is essential to develop efficient algorithms to solve a very broad class of TV-regularized problems.

Methods: In this paper, we propose an efficient algorithm referred to as the fast linearized preconditioned alternating direction method of multipliers (FLPADMM), to solve an augmented TV-regularized model that adds a quadratic term to enforce image smoothness. Because of the separable structure of this model, FLPADMM decomposes the convex problem into two subproblems. Each subproblem can be alternatively minimized by augmented Lagrangian function. Furthermore, a linearized strategy and multistep weighted scheme can be easily combined for more effective image recovery.

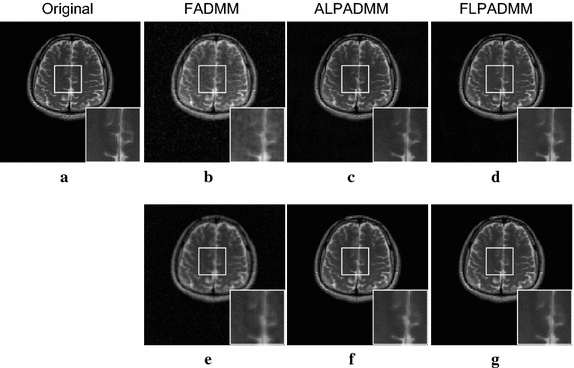
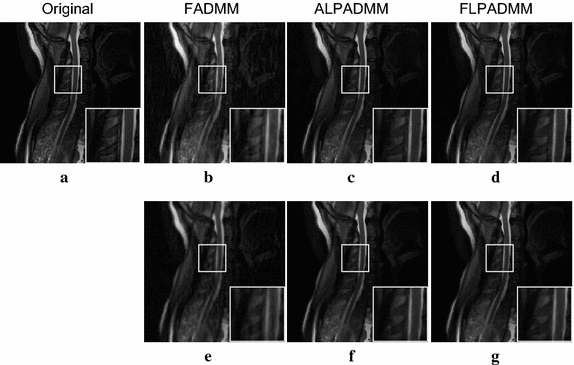
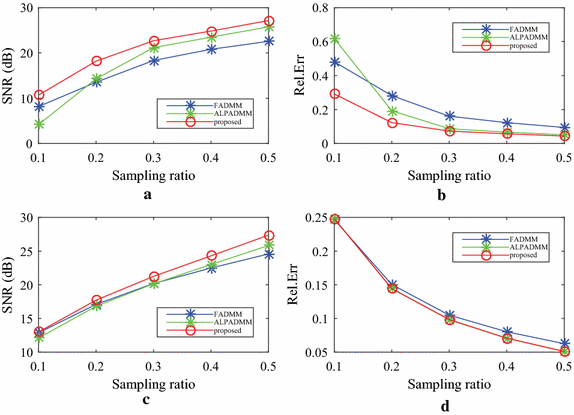
Results: The method of the present study showed improved accuracy and efficiency, in comparison to other methods. Furthermore, the experiments conducted on in vivo data showed that our algorithm achieved a higher signal-to-noise ratio (SNR), lower relative error (Rel.Err), and better structural similarity (SSIM) index in comparison to other state-of-the-art algorithms.

Conclusions: Extensive experiments demonstrate that the proposed algorithm exhibits superior performance in accuracy and efficiency than conventional compressed sensing MRI algorithms.

Keywords: Alternating direction method of multipliers; Compressed sensing MRI; Image reconstruction; Total variation.

Fig. 1

MR images. (a) Shepp–Logan phantom (b) human brain1 image (c) human brain2 image (d) human spine image

Fig. 2

Sampling masks. a pseudo-Gaussian mask at 15% sampling rate, b pseudo-radial mask at 18% sampling rate

Fig. 3

Analysis to determine the optimum regularization parameters for human brain1 data using a pseudo-Gaussian mask at a sampling rate of 25%

Fig. 4

Results of three methods under a pseudo-Gaussian mask with 20% sampling. a Original Shepp–Logan phantom, b FADMM, c ALPADMM, d proposed FLPADMM, and e–g error map of b–d, respectively

Fig. 5

Reconstructed images and zoomed-in regions among the state-of-the-art MR image reconstruction algorithms using a pseudo-Gaussian mask (first row) and pseudo-radial mask (second row) with 25% sampling. a Original human brain1 image, b, e FADMM, c, f ALPADMM, d, g FLPADMM

Fig. 6

Reconstructed images and zoomed-in regions among the state-of-the-art MR image reconstruction algorithms using a pseudo-Gaussian mask (first row) and pseudo-radial mask (second row) with 25% sampling. a Original human brain1 image, b, e FADMM, c, f ALPADMM, d, g FLPADMM

Fig. 7

Comparison results of human brain1 data using a pseudo-Gaussian mask (first row) and pseudo-radial mask (second row). a, c SNR (dB) vs sampling ratio, b, d Rel.Err vs sampling ratio

Fig. 8

Comparison results of human brain2 data using a pseudo-Gaussian mask (first row) and pseudo-radial mask (second row). a, c SNR (dB) vs sampling ratio, b, d Rel.Err vs sampling ratio

Fig. 9

Reconstructed images and zoomed-in regions among the state-of-the-art MR image reconstruction algorithms using a pseudo-Gaussian mask (first row) and pseudo-radial mask (second row) with 25% sampling. a Original human brain1 image, b, e FADMM, c, f ALPADMM, d, g FLPADMM

Fig. 10

Comparison results of human spine data using a pseudo-Gaussian mask (first row) and pseudo-radial mask (second row). a, c SNR (dB) vs sampling ratio, b, d Rel.Err vs sampling ratio