Pointwise error estimates in localization microscopy
- PMID: 28466844
- PMCID: PMC5418599
- DOI: 10.1038/ncomms15115
Pointwise error estimates in localization microscopy
Abstract
Pointwise localization of individual fluorophores is a critical step in super-resolution localization microscopy and single particle tracking. Although the methods are limited by the localization errors of individual fluorophores, the pointwise localization precision has so far been estimated using theoretical best case approximations that disregard, for example, motion blur, defocus effects and variations in fluorescence intensity. Here, we show that pointwise localization precision can be accurately estimated directly from imaging data using the Bayesian posterior density constrained by simple microscope properties. We further demonstrate that the estimated localization precision can be used to improve downstream quantitative analysis, such as estimation of diffusion constants and detection of changes in molecular motion patterns. Finally, the quality of actual point localizations in live cell super-resolution microscopy can be improved beyond the information theoretic lower bound for localization errors in individual images, by modelling the movement of fluorophores and accounting for their pointwise localization uncertainty.
Conflict of interest statement
The authors declare no competing financial interests.
Figures

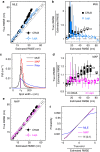
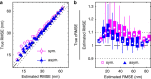
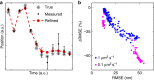
 <0.9, using symmetric and asymmetric Gaussian spot models for MAP localization and Laplace precision estimates. Dashed and dotted lines indicate 0% and ±10% bias, respectively. (a) True and estimated RMSEs for each imaging condition with error bars (mostly smaller than symbols) showing bootstrap s.e.m. (b) Conditional RMSE (cRMSE) normalized by estimated RMSE. Symbols, boxes, and lines show the median, 25% and 75% quantiles, and the whole span for all localization conditions.
<0.9, using symmetric and asymmetric Gaussian spot models for MAP localization and Laplace precision estimates. Dashed and dotted lines indicate 0% and ±10% bias, respectively. (a) True and estimated RMSEs for each imaging condition with error bars (mostly smaller than symbols) showing bootstrap s.e.m. (b) Conditional RMSE (cRMSE) normalized by estimated RMSE. Symbols, boxes, and lines show the median, 25% and 75% quantiles, and the whole span for all localization conditions.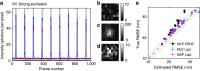
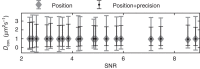

References
-
- Sage D. et al.. Quantitative evaluation of software packages for single-molecule localization microscopy. Nat. Methods 12, 717–724 (2015). - PubMed
-
- Rieger B. & Stallinga S. The lateral and axial localization uncertainty in super-resolution light microscopy. ChemPhysChem. 15, 664–670 (2014). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

