Long-range temporal correlations in neural narrowband time-series arise due to critical dynamics
- PMID: 28472078
- PMCID: PMC5417502
- DOI: 10.1371/journal.pone.0175628
Long-range temporal correlations in neural narrowband time-series arise due to critical dynamics
Abstract
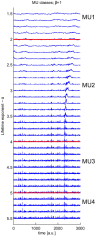
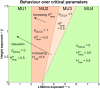
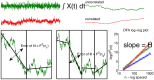
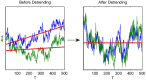
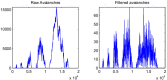
We show theoretically that the hypothesis of criticality as a theory of long-range fluctuation in the human brain may be distinguished from the theory of passive filtering on the basis of macroscopic neuronal signals such as the electroencephalogram, using novel theory of narrowband amplitude time-series at criticality. Our theory predicts the division of critical activity into meta-universality classes. As a consequence our analysis shows that experimental electroencephalography data favours the hypothesis of criticality in the human brain.
Conflict of interest statement
Figures

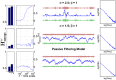
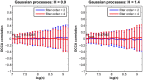
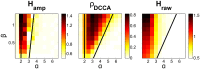
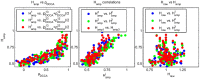
Similar articles
-
Random graph theory and neuropercolation for modeling brain oscillations at criticality.Curr Opin Neurobiol. 2015 Apr;31:181-8. doi: 10.1016/j.conb.2014.11.005. Epub 2014 Dec 1. Curr Opin Neurobiol. 2015. PMID: 25460075 Review.
-
Brain criticality predicts individual levels of inter-areal synchronization in human electrophysiological data.Nat Commun. 2023 Aug 7;14(1):4736. doi: 10.1038/s41467-023-40056-9. Nat Commun. 2023. PMID: 37550300 Free PMC article.
-
Stability of neuronal avalanches and long-range temporal correlations during the first year of life in human infants.Brain Struct Funct. 2020 Apr;225(3):1169-1183. doi: 10.1007/s00429-019-02014-4. Epub 2020 Feb 24. Brain Struct Funct. 2020. PMID: 32095901 Free PMC article.
-
Neurofeedback Tunes Scale-Free Dynamics in Spontaneous Brain Activity.Cereb Cortex. 2017 Oct 1;27(10):4911-4922. doi: 10.1093/cercor/bhw285. Cereb Cortex. 2017. PMID: 27620975
-
Comparative approximations of criticality in a neural and quantum regime.Prog Biophys Mol Biol. 2017 Dec;131:445-462. doi: 10.1016/j.pbiomolbio.2017.09.007. Epub 2017 Oct 12. Prog Biophys Mol Biol. 2017. PMID: 29031703 Review.
Cited by
-
Long-range temporal correlation in Auditory Brainstem Responses to Spoken Syllable/da/.Sci Rep. 2019 Feb 11;9(1):1751. doi: 10.1038/s41598-018-38215-w. Sci Rep. 2019. PMID: 30741968 Free PMC article.
-
Optimal Organization of Functional Connectivity Networks for Segregation and Integration With Large-Scale Critical Dynamics in Human Brains.Front Comput Neurosci. 2021 Mar 31;15:641335. doi: 10.3389/fncom.2021.641335. eCollection 2021. Front Comput Neurosci. 2021. PMID: 33867963 Free PMC article.
References
-
- Kuntz MC, Sethna JP. Noise in disordered systems: The power spectrum and dynamic exponents in avalanche models. Physical Review B. 2000;62(17):11699 10.1103/PhysRevB.62.11699 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

