Parameter identifiability analysis and visualization in large-scale kinetic models of biosystems

Abstract

Background: Kinetic models of biochemical systems usually consist of ordinary differential equations that have many unknown parameters. Some of these parameters are often practically unidentifiable, that is, their values cannot be uniquely determined from the available data. Possible causes are lack of influence on the measured outputs, interdependence among parameters, and poor data quality. Uncorrelated parameters can be seen as the key tuning knobs of a predictive model. Therefore, before attempting to perform parameter estimation (model calibration) it is important to characterize the subset(s) of identifiable parameters and their interplay. Once this is achieved, it is still necessary to perform parameter estimation, which poses additional challenges.

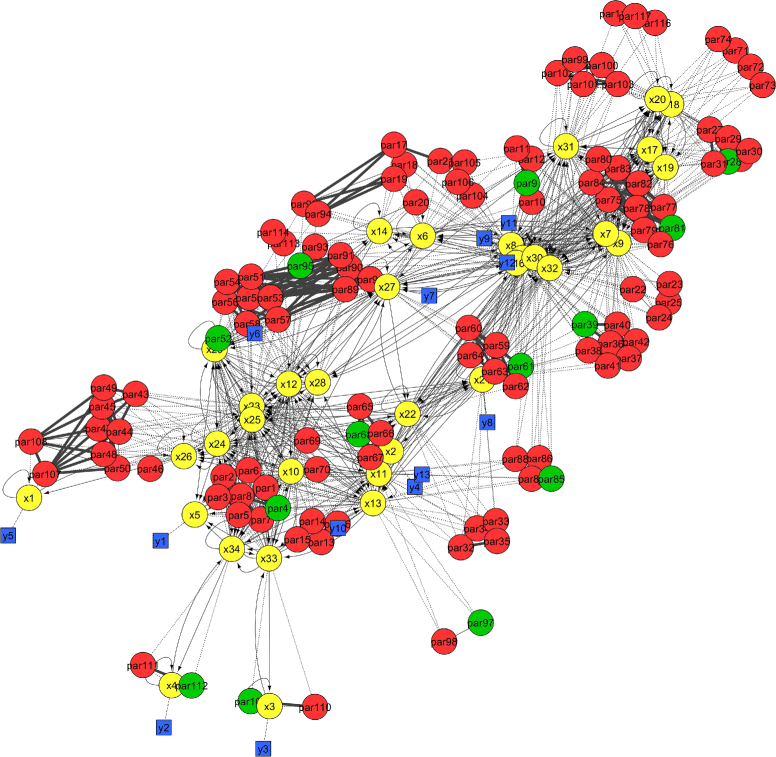
Methods: We present a methodology that (i) detects high-order relationships among parameters, and (ii) visualizes the results to facilitate further analysis. We use a collinearity index to quantify the correlation between parameters in a group in a computationally efficient way. Then we apply integer optimization to find the largest groups of uncorrelated parameters. We also use the collinearity index to identify small groups of highly correlated parameters. The results files can be visualized using Cytoscape, showing the identifiable and non-identifiable groups of parameters together with the model structure in the same graph.

Results: Our contributions alleviate the difficulties that appear at different stages of the identifiability analysis and parameter estimation process. We show how to combine global optimization and regularization techniques for calibrating medium and large scale biological models with moderate computation times. Then we evaluate the practical identifiability of the estimated parameters using the proposed methodology. The identifiability analysis techniques are implemented as a MATLAB toolbox called VisId, which is freely available as open source from GitHub ( https://github.com/gabora/visid ).

Conclusions: Our approach is geared towards scalability. It enables the practical identifiability analysis of dynamic models of large size, and accelerates their calibration. The visualization tool allows modellers to detect parts that are problematic and need refinement or reformulation, and provides experimentalists with information that can be helpful in the design of new experiments.

Keywords: Dynamic models; Global optimization; Identifiability; Overfitting; Parameter estimation; Regularization.

Fig. 1

TGF- β model: panel a shows the model sensitivities with respect to the parameters in logarithmic scale. In panel b the maximum number of identifiable parameters is depicted depending on the collinearity threshold. The group-size does not change much by the threshold. The red vertical line indicates our choice (CI =20) for the further analysis. In panel c the mathematical model is depicted. Nodes indicate states (yellow), identifiable (green) and not identifiable (red) parameters, and observables (blue). In panel d the interplay among the collinear parameters are indicated. There are 5 groups of parameters: in the first 4 groups triplets of parameters show large collinearity, while in the fifth group 5 parameters are collinear

Fig. 2

Circadian clock in Arabidopsis thaliana: panel a shows the model sensitivities with respect to parameters in logarithmic scale. In panel b the maximum number of identifiable parameters is depicted as a function of the collinearity threshold. The red vertical line indicates our choice of threshold (CI =20) used for further analysis. In panel c the interplay among the collinear parameters is indicated up to groups of 3 parameters. In panel d the mathematical model is depicted. Nodes indicate states (yellow), identifiable (green) and not identifiable (red) parameters, and observables (blue). Highly correlated parameter pairs are connected by undirected edges

Fig. 3

Representation of the connections in the B2 model using the network diagram formalism. Nodes indicate states (yellow), identifiable (green) and not identifiable (red) parameters, observables (blue), and inputs (grey). The source file of this figure is provided with the VisId toolbox; using Cytoscape, the user can navigate through it and zoom on different areas to improve the visibility

Fig. 4

Representation of the connections in the B4 model using the network diagram formalism. Nodes indicate states (yellow), identifiable (green) and not identifiable (red) parameters, observables (blue), and inputs (grey)

Fig. 5

Visualization of the relationships among highly collinear parameters in the B4 model. The figure shows small groups, whose sizes range between 2 and 10 parameters. Unidentifiable parameters are shown in red; identifiable parameters in green. Highly correlated pairs are connected by lines