Molecular Knots
- PMID: 28477423
- PMCID: PMC5582600
- DOI: 10.1002/anie.201702531
Molecular Knots
Abstract
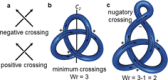
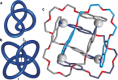
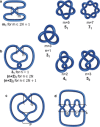
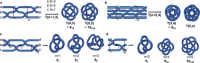
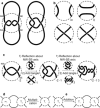
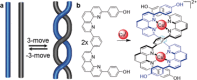
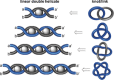
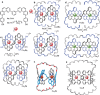
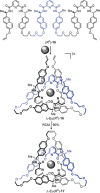
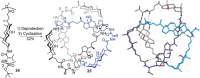
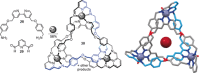
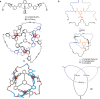
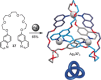
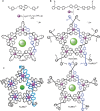
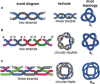
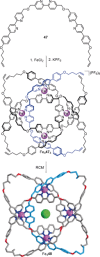
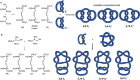
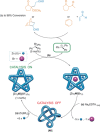
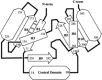
The first synthetic molecular trefoil knot was prepared in the late 1980s. However, it is only in the last few years that more complex small-molecule knot topologies have been realized through chemical synthesis. The steric restrictions imposed on molecular strands by knotting can impart significant physical and chemical properties, including chirality, strong and selective ion binding, and catalytic activity. As the number and complexity of accessible molecular knot topologies increases, it will become increasingly useful for chemists to adopt the knot terminology employed by other disciplines. Here we give an overview of synthetic strategies towards molecular knots and outline the principles of knot, braid, and tangle theory appropriate to chemistry and molecular structure.
Keywords: interlocked molecules; molecular knots; supramolecular chemistry; template synthesis; topology.
© 2017 The Authors. Published by Wiley-VCH Verlag GmbH & Co. KGaA.
Figures














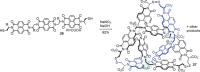





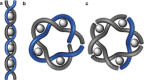






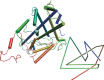
References
-
- Turner J. C., van de Griend P. in History and science of knots, World Scientific, Singapore, 1996.
-
- Huurre M. in 9000 vuotta Suomen esihistoriaa, Otava, Helsinki, 1979, p. 18.
-
- Mann C. C., Science 2005, 309, 1008–1009. - PubMed
-
- Herzfeld C., Wattana: An Orangutan in Paris (translated by O. Y. Martin, R. D. Martin), University of Chicago Press, Chicago, 2016, p. 87.
-
- Crook J. H., Ibis 1960, 1–25.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

