Integrated Analysis of Intracellular Dynamics of MenaINV Cancer Cells in a 3D Matrix

Abstract

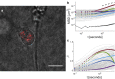
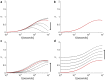
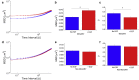
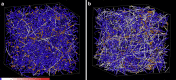
The intracellular environment is composed of a filamentous network that exhibits dynamic turnover of cytoskeletal components and internal force generation from molecular motors. Particle tracking microrheology enables a means to probe the internal mechanics and dynamics. Here, we develop an analytical model to capture the basic features of the active intracellular mechanical environment, including both thermal and motor-driven effects, and show consistency with a diverse range of experimental microrheology data. We further perform microrheology experiments, integrated with Brownian dynamics simulations of the active cytoskeleton, on metastatic breast cancer cells embedded in a three-dimensional collagen matrix with and without the presence of epidermal growth factor to probe the intracellular mechanical response in a physiologically mimicking scenario. Our results demonstrate that EGF stimulation can alter intracellular stiffness and power output from molecular motor-driven fluctuations in cells overexpressing an invasive isoform of the actin-associated protein Mena.

Figure 1

Intracellular fluctuations of cell in a 3D matrix. (a) An MDA-MB-231 cell, with labeled mitochondria (red), is embedded inside a 2 mg/mL collagen matrix. (b) Profiles of in-plane MSD versus time interval t of intracellular fluctuations from mitochondria tracers (gray curves) display heterogeneity. Different colored dots highlight typical MSDs with distinct characteristics. Dashed line is proportional to t. Note that the average MSD of stuck fluorescent beads on glass is ∼10⁻⁴μm², as shown by the lower black curve. Error bars are mean ± SE (n = 40). (c) Profiles display the logarithmic derivatives, beta's, of the MSD’s shown in (b), with corresponding colors. Scale bars represent 20 μm.

Figure 2

MSD versus active parameters. (a) Altering s₀ leads to a modulation in the onset of the plateau at long timescales. (b) Altering B shifts the magnitude of the MSD. (c) Altering A modulates the onset of the high slope regime at long timescales. (d) Altering α modulates the logarithmic slope at both the short and long timescales. The arrow indicates the direction of increasing the parameter of interest. The red curve is a common reference curve for (a–d) and has parameter values of A = 1.5 k_BT [s⁻¹], B = 2 [Pa s^−α], α = 0, s₀ = 1/30 Hz, dimensions = 2, T = 310 K, r_tracer = 70 nm. The dashed blue line scales as t and the dotted blue line scales as t².

Figure 3

β versus active parameters. (a–d) These panels correspond to (a–d) in Fig. 2. (a) Increasing s₀ shortens the timescale when β at long timescales returns to the value of β at short timescales. (b) Increasing B does not alter β. (c) Altering A modulates how quickly β increases at long timescales. (d) Altering α shifts the magnitude of β. The arrow indicates the direction of increasing the parameter of interest, and the red curve indicates the identical reference for (a–d) with parameter values indicated in the caption of Fig. 2.

Figure 4

Impact of EGF stimulation on MDA-MB-231 breast cancer cells with (a–c) and without (d–f) overexpression of MenaINV. (a) Average 2D MSD of MenaINV overexpressing cells without EGF (blue) and with 5 nM EGF (red). Circles are data and curves are fits to Eq. 14. The R² values for the fits are 0.9986 for without EGF and 0.9956 for with EGF. (b) MSDs at t = 0.05 s without EGF (blue) (0.0076 ± 0.0004 μm², n = 157) and with EGF (red) (0.0116 ± 0.0005 μm², n = 162). (c) β at t = 1 s without EGF (blue) (0.37 ± 0.02, n = 157) and with EGF (red) (0.27 ± 0.02, n = 162). (d) Average 2D MSD of non-MenaINV overexpressing cells without EGF (blue) and with 5 nM EGF (red). Circles are data and curves are fits to Eq. 14. The R² values for the fits are 0.9994 for without EGF and 0.9992 for with EGF. (e) MSDs at t = 0.05 s without EGF (blue) (0.0085 ± 0.0004 μm², n =148) and with EGF (red) (0.0079 ± 0.0004 μm², n = 169). (f) β at t = 1 s without EGF (blue) (0.45 × 0.02, n =148) and with EGF (red) (0.43 ± 0.02, n = 169). Asterisk indicates p < 0.01, n is the number of particles tracked in each case, and error bars and values indicate mean ± SE.

Figure 5

Brownian dynamics simulations of active actin networks in 3D. Networks with actin nucleation rates of (a) 0.1 and (b) 0.01 μM⁻¹ s⁻¹. All simulated networks have 25 M actin, 1% ACPs to actin, and 1% myosin II motors to actin in a 3 × 3 × 3 μm³ domain with periodic boundary conditions. The actin turnover (treadmilling) rate is set to 300 s⁻¹, which is sufficient to maintain homogeneous rather than clustered networks in these simulations. Orange represents motors, yellow represents ACPs, and fibers represent actin filaments. The color scale applies to the actin filaments and represents a tensile force range from 0 (blue) to 100 pN (red).

Figure 6

The impact of actin nucleation rates on actin network mechanics and dynamics. (a) Stress profiles over time for cross-linked actomyosin networks with varying nucleation rates. All simulated networks have 25 μM actin, 1% ACPs to actin, and 1% myosin motors to actin. The actin turnover rate is set to 300 s⁻¹. Stresses are calculated by averaging the sum of the normal tensile forces per unit area across eight 3 × 3 μm² cross sections along each dimension of the domain. (b) Normalized distributions of stress fluctuations from the mean over 1 s time intervals from the data shown in (a). Open circles are from computational data and solid curves are Gaussian fits with corresponding means and SDs. (c) Average stress versus nucleation rate. Upper and lower bounds represent the stress fluctuations from the mean over 1 s as calculated from the SD of each of the stress fluctuation distributions in (b). Inset shows average filament length versus nucleation rate. (d) Normalized stress autocorrelation. Open squares are simulation data points and solid curves are fits to exponential decays with time constants between 3 and 5 s. In (a), (b), and (d), blue, red, yellow, and purple correspond to nucleation rates of 0.01, 0.05, 0.1, and 0.2 μM⁻¹ s⁻¹, respectively.