Correlated velocity models as a fundamental unit of animal movement: synthesis and applications

Abstract

Background: Continuous time movement models resolve many of the problems with scaling, sampling, and interpretation that affect discrete movement models. They can, however, be challenging to estimate, have been presented in inconsistent ways, and are not widely used.

Methods: We review the literature on integrated Ornstein-Uhlenbeck velocity models and propose four fundamental correlated velocity movement models (CVM's): random, advective, rotational, and rotational-advective. The models are defined in terms of biologically meaningful speeds and time scales of autocorrelation. We summarize several approaches to estimating the models, and apply these tools for the higher order task of behavioral partitioning via change point analysis.

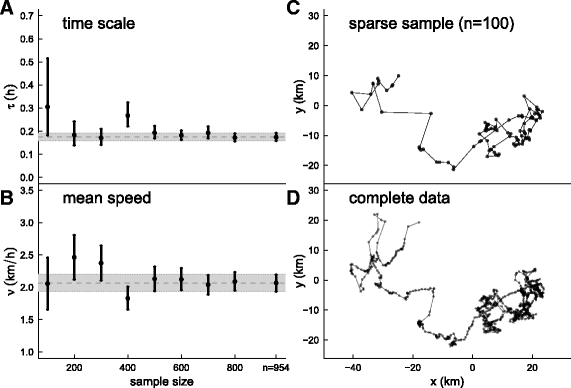
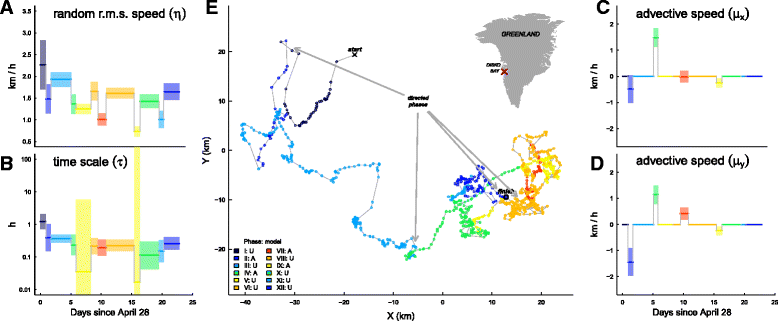
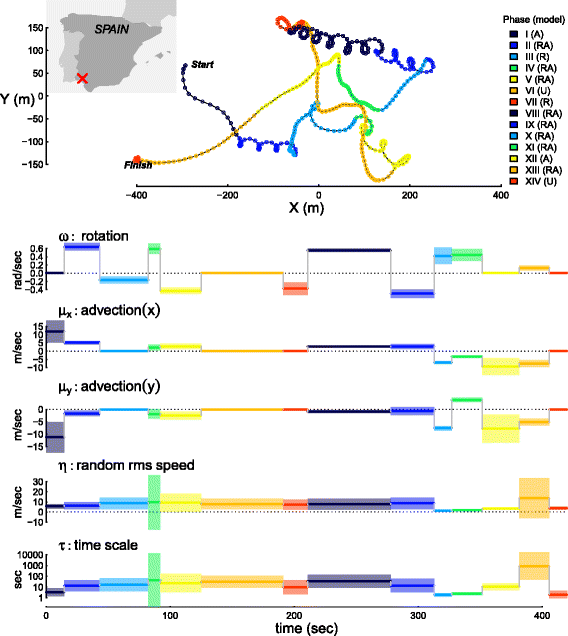
Results: An array of simulation illustrate the precision and accuracy of the estimation tools. An analysis of a swimming track of a bowhead whale (Balaena mysticetus) illustrates their robustness to irregular and sparse sampling and identifies switches between slower and faster, and directed vs. random movements. An analysis of a short flight of a lesser kestrel (Falco naumanni) identifies exact moments when switches occur between loopy, thermal soaring and directed flapping or gliding flights.

Conclusions: We provide tools to estimate parameters and perform change point analyses in continuous time movement models as an R package (smoove). These resources, together with the synthesis, should facilitate the wider application and development of correlated velocity models among movement ecologists.

Keywords: Balaena mysticetus; Correlated random walk; Correlated velocity movement; Falco naumanni; Integrated Ornstein-Uhlenbeck process; Thermal soaring; Velocity autocovariance function.

Fig. 1

Four sample trajectories (left panels) and corresponding velocity auto-covariance functions (right panels) of CVM movement models. In all trajectories, the characteristic time scale τ=5, the random mean squared speed η=3 and the sampling intervals are 0.01. Start and end of each trajectory is represented with filled circles and x’s, respectively. Regions of darker and lighter grey within the track indicate locations where the speed is slower or faster. In panel a, the mean velocity and rotation are equal to 0, in panels b and d, there is a mean component of velocity μ _x=2, and in panels c and d there is a rotational component ω=2. In the right panels, black lines are the empirical estimates of the velocity auto-covariance function (EVAF), the red dashed line is the theoretical prediction (Equation A15), and the horizontal dashed grey line is the predicted asymptote |μ ²|, reflecting the advective term in the process

Fig. 2

Results of estimation of UCVM parameters for the Greenland bowhead whale (see inset in Fig. 3). Panels a and b indicate the full position likelihood estimates of time scale τ and speed ν for a range of random subsamplings from 100 observations (illustrated in panel c) to the complete dataset with 954 observations (panel d) intervals for the estimates. The vertical bars indicate the 95% confidence interval of the estimate, while the horizontal grey bar shows the point estimate and confidence intervals for the compete data (i.e. n=954) for comparison

Fig. 3

Change point analysis of the bowhead track in Disko Bay, Greenland (inset map). In the left panels are the estimates of (a) random r.m.s. speed η and (b) time scale τ. On the right panels, estimates of the (c) x and (d) y components of the advective velocity μ. These are non-zero only for those four phases (II, IV, VII, IX) for which the advective CVM was selected over the unbiased CVM. Each color corresponds to a particular phase, matching the mapped track (e), with enumerated phases (legend in panel (e)) reporting whether the movement phase was determined to be unbiased (U) or advective (a). The arrows point to the first location of the four directed phases

Fig. 4

Change point analysis of a lesser kestrel’s 7 min flight in southwestern Spain (inset map). The upper panel illustrates the track of the flight, with the colors indicating 14 identified phases starting with the dark blue (phase I, at the indicated start) and cycling twice through high contrast rainbow colors to the final red roost (phase XIV, finish). The legend indicates whether a particular portion of the track contained a significant advective (a) or rotational component(R), both (RA), or neither (U). The lower panels indicate the estimated values of the five RACVM parameters for each phase over time, with the width of the bars indicating 95% confidence intervals. Note that positive and negative values for ω represent clockwise and counterclockwise rotation, respectively, and values of 0 for ω, μ _x and μ _y indicate that a non-rotational and/or advective model was selected