Linkage disequilibrium matches forensic genetic records to disjoint genomic marker sets
- PMID: 28507140
- PMCID: PMC5465933
- DOI: 10.1073/pnas.1619944114
Linkage disequilibrium matches forensic genetic records to disjoint genomic marker sets
Abstract
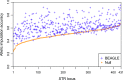
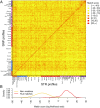
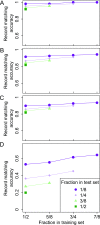
Combining genotypes across datasets is central in facilitating advances in genetics. Data aggregation efforts often face the challenge of record matching-the identification of dataset entries that represent the same individual. We show that records can be matched across genotype datasets that have no shared markers based on linkage disequilibrium between loci appearing in different datasets. Using two datasets for the same 872 people-one with 642,563 genome-wide SNPs and the other with 13 short tandem repeats (STRs) used in forensic applications-we find that 90-98% of forensic STR records can be connected to corresponding SNP records and vice versa. Accuracy increases to 99-100% when ∼30 STRs are used. Our method expands the potential of data aggregation, but it also suggests privacy risks intrinsic in maintenance of databases containing even small numbers of markers-including databases of forensic significance.
Keywords: forensic DNA; genomic privacy; imputation; population genetics; record matching.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
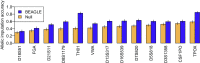







References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

