Continuous variables logic via coupled automata using a DNAzyme cascade with feedback

Abstract

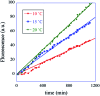
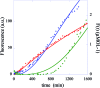
The concentration of molecules can be changed by chemical reactions and thereby offer a continuous readout. Yet computer architecture is cast in textbooks in terms of binary valued, Boolean variables. To enable reactive chemical systems to compute we show how, using the Cox interpretation of probability theory, one can transcribe the equations of chemical kinetics as a sequence of coupled logic gates operating on continuous variables. It is discussed how the distinct chemical identity of a molecule allows us to create a common language for chemical kinetics and Boolean logic. Specifically, the logic AND operation is shown to be equivalent to a bimolecular process. The logic XOR operation represents chemical processes that take place concurrently. The values of the rate constants enter the logic scheme as inputs. By designing a reaction scheme with a feedback we endow the logic gates with a built in memory because their output then depends on the input and also on the present state of the system. Technically such a logic machine is an automaton. We report an experimental realization of three such coupled automata using a DNAzyme multilayer signaling cascade. A simple model verifies analytically that our experimental scheme provides an integrator generating a power series that is third order in time. The model identifies two parameters that govern the kinetics and shows how the initial concentrations of the substrates are the coefficients in the power series.

Fig. 1. The three layers of DNAzyme–hairpin (left) and their representation as three concatenated logic units (right). The reaction starts due to D₃ and H₂ initially present in the system. D₃ is regenerated, and this is the feedback that is also shown in the logic scheme. Only H₂ is consumed and is initially present in excess. The top layer generates D₂, which is an input to the second layer, and this is the feed forward shown in the logic scheme. D₂ reacts with H₁, which needs to be present initially, preferably in excess. D₁ is delivered to the bottom layer as a feed forward. D₁ hybridizes with FQ to release the fluorophore that provides the output. The cycle continues by the regeneration of D₁. See text for more details.

Fig. 2. A one layer operation. The measured fluorescence at three different temperatures, cited in degrees C (see inset) vs. time. The straight lines are fits to the data. The kinetic scheme (eqn (1)) shows (see Section II of the ESI†) that after an induction period the fluorescence increases linearly with time with a rate constant that increases with temperature.

Fig. 3. The experimentally measured fluorescence for the one layer system (red diamonds), the two layer system (blue diamonds) and the three layer system (green diamonds). Also shown as continuous curves are numerical fits using the kinetic scheme (eqn (1)), one layer, and of Section I of the ESI. The numerical integration of the non-linear rate equations was done using a Runge–Kutta fifth order scheme. The values of initial concentrations are as in the experiments and the rate constants are from Table 1. Each point shown as experimental is an average over three measurements. The initial concentrations (in μmol) are: one layer system [D₁(t = 0)] = 0.66 and [FQ(t = 0)] = 4, two layer system: [D₁(t = 0)] = 0, [D₂(t = 0)] = 0.66, [FQ(t = 0)] = 4, [H₁(t = 0)] = 4, three layer system: [D₁(t = 0)] = 0, [D₂(t = 0)] = 0, [D₃(t = 0) = 0.66], [FQ(t = 0)] = 4, [H₁(t = 0)] = 4, [H₂(t = 0) = 4].

Scheme 1. A microscopic view of an AND between two molecules implemented by the progress of a bimolecular event.