An Introduction to Infinite HMMs for Single-Molecule Data Analysis

Abstract

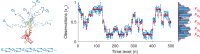
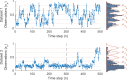
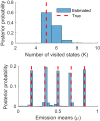
The hidden Markov model (HMM) has been a workhorse of single-molecule data analysis and is now commonly used as a stand-alone tool in time series analysis or in conjunction with other analysis methods such as tracking. Here, we provide a conceptual introduction to an important generalization of the HMM, which is poised to have a deep impact across the field of biophysics: the infinite HMM (iHMM). As a modeling tool, iHMMs can analyze sequential data without a priori setting a specific number of states as required for the traditional (finite) HMM. Although the current literature on the iHMM is primarily intended for audiences in statistics, the idea is powerful and the iHMM's breadth in applicability outside machine learning and data science warrants a careful exposition. Here, we explain the key ideas underlying the iHMM, with a special emphasis on implementation, and provide a description of a code we are making freely available. In a companion article, we provide an important extension of the iHMM to accommodate complications such as drift.

Figure 1

A synthetic time trace illustrating measurements of a hypothetical biomolecule that undergoes conformational transitions. (Left) The state space consists of conformations depicted discretely as ${\sigma }_1,{\sigma }_2,\dots$. (Middle) Time series of noisy observations, $x_n$, produced by the biomolecule (blue) and the corresponding noiseless trace (red). Over the time course of the measurements, the biomolecule attains only conformations ${\sigma }_1$–${\sigma }_5$, though additional conformations might be visited at subsequent times. For the sake of concreteness only, we label these states in order of appearance from 1 through 5. (Right) Binning the collected observations reveals “emission distributions,” $F_{{\sigma }_k}$, associated with each conformation. These distributions are highlighted with red lines. The centers (mean values) of the emission distributions are used to obtain the noiseless trace in the middle panel. The illustration on the left is created using data from (47) (PDB: 2N4G). To see this figure in color, go online.

Figure 2

Graphical representation of the HMM. In the HMM, a biomolecule of interest transitions between unobserved states $s_n$ according to the probability vectors ${\tilde{\pi }}_{s_n}$ and generates observations $x_n$ according to the probability distributions $F_{s_n}$ that depend on the parameter ${\varphi }_{s_n}$. Here, following convention, the $x_n$ values are shaded to denote that these quantities are observed, whereas the $s_n$ values are hidden. Arrows denote the dependences among the model variables and red lines denote the model parameters. To see this figure in color, go online.

Figure 3

Graphical representation of the iHMM. The hidden Markov model that formulates the observations to be analyzed (black lines) is shown together with its priors (red lines). For completeness, we also show the concentration parameters α and γ and the prior probability distribution on the emission parameters, H, that fully characterize the iHMM. The key difference from the HMM shown in Fig. 2 is that now the model parameters ${\tilde{\pi }}_{{\sigma }_k}$ and ${\varphi }_{{\sigma }_k}$ are treated as random variables similar to the hidden states, $s_n$, and observations, $x_n$. For details, see the main text. To see this figure in color, go online.

Figure 4

Synthetic data sets resembling a hypothetical biomolecule undergoing transitions between discrete states that we analyzed with the iHMM. (Left) Time series $\overline{x}=\left(x_1,\dots ,x_N\right)$ of noisy observations. During the measuring period, the biomolecule attains five conformations, ${\sigma }_1,\dots ,{\sigma }_5$. The number of conformations are a priori unknown and the iHMM seeks to determine the probability over the number of states, as well as their properties, given the data available. In data set 1, the biomolecule transitions often through every state. By contrast, in data set 2, transitions to some states are rare. As a result, all states in data set 1 are almost equally visited throughout the experiment time course, whereas in data set 2, higher states are visited, by chance, only toward the end of the trace. (Right) The corresponding emission distributions, $F_{{\sigma }_k}$, as obtained by simply binning the observations (blue) and plotting the exact ones used for the simulations (red). For both data sets, the emission distributions show significant overlap. In all panels, dotted lines indicate the exact mean values, ${\mu }_{{\sigma }_k}$, of the emission distributions. To see this figure in color, go online.

Figure 5

After some iterations, the sampler used in the iHMM to analyze data set 1 of Fig. 4 eventually converges to the correct number of states. The number of visited states, $K^{\left(r\right)}$ (top), and the means of the emission distributions, ${\mu }_{{\sigma }_k}^{\left(r\right)}$ (bottom), change throughout the sampler’s iterations. Unlike the HMM, which uses a finite and fixed state space, the iHMM learns the number of available states and grows/shrinks the state space as required by the data.

Figure 6

We may use samples from the iHMM posterior probability to infer the size of the state space and the location of each state. In particular, we illustrate histograms for $\mathbb{P}\left(K|\overline{x}\right)$ (top) and $\mathbb{P}\left({\mu }_{{\sigma }_k}|\overline{x}\right)$ (bottom) using data set 1 of Fig. 4. In both panels, dashed lines indicate the exact (ground-truth) values used to produce the data in Fig. 4. To see this figure in color, go online.

Figure 7

We may use the iHMM to estimate portions of the complete state space such as those contained in different segments of data set 2 provided in Fig. 4. (Upper) Estimated noiseless traces for two cases: 1) using a limited segment of the full trace; and 2) using the full trace. Although only the latter case allows an estimate of all five states, both cases provide similar estimates over those states that they mutually visit. (Lower) Corresponding estimates of the number of states contained in each trace. To see this figure in color, go online.