New Continuum Approaches for Determining Protein-Induced Membrane Deformations
- PMID: 28538153
- PMCID: PMC5448241
- DOI: 10.1016/j.bpj.2017.03.040
New Continuum Approaches for Determining Protein-Induced Membrane Deformations
Abstract
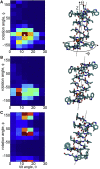
The influence of the membrane on transmembrane proteins is central to a number of biological phenomena, notably the gating of stretch activated ion channels. Conversely, membrane proteins can influence the bilayer, leading to the stabilization of particular membrane shapes, topological changes that occur during vesicle fission and fusion, and shape-dependent protein aggregation. Continuum elastic models of the membrane have been widely used to study protein-membrane interactions. These mathematical approaches produce physically interpretable membrane shapes, energy estimates for the cost of deformation, and a snapshot of the equilibrium configuration. Moreover, elastic models are much less computationally demanding than fully atomistic and coarse-grained simulation methodologies; however, it has been argued that continuum models cannot reproduce the distortions observed in fully atomistic molecular dynamics simulations. We suggest that this failure can be overcome by using chemically and geometrically accurate representations of the protein. Here, we present a fast and reliable hybrid continuum-atomistic model that couples the protein to the membrane. We show that the model is in excellent agreement with fully atomistic simulations of the ion channel gramicidin embedded in a POPC membrane. Our continuum calculations not only reproduce the membrane distortions produced by the channel but also accurately determine the channel's orientation. Finally, we use our method to investigate the role of membrane bending around the charged voltage sensors of the transient receptor potential cation channel TRPV1. We find that membrane deformation significantly stabilizes the energy of insertion of TRPV1 by exposing charged residues on the S4 segment to solution.
Copyright © 2017 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures




References
-
- Zimmerberg J., Kozlov M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006;7:9–19. - PubMed
-
- Andersen O.S., Koeppe R.E., 2nd, Koeppe E. Bilayer thickness and membrane protein function: an energetic perspective. Annu. Rev. Biophys. Biomol. Struct. 2007;36:107–130. - PubMed
-
- Perozo E., Cortes D.M., Martinac B. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature. 2002;418:942–948. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

