Cure modeling in real-time prediction: How much does it help?

Abstract

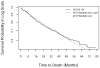
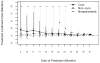
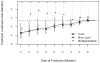
Various parametric and nonparametric modeling approaches exist for real-time prediction in time-to-event clinical trials. Recently, Chen (2016 BMC Biomedical Research Methodology 16) proposed a prediction method based on parametric cure-mixture modeling, intending to cover those situations where it appears that a non-negligible fraction of subjects is cured. In this article we apply a Weibull cure-mixture model to create predictions, demonstrating the approach in RTOG 0129, a randomized trial in head-and-neck cancer. We compare the ultimate realized data in RTOG 0129 to interim predictions from a Weibull cure-mixture model, a standard Weibull model without a cure component, and a nonparametric model based on the Bayesian bootstrap. The standard Weibull model predicted that events would occur earlier than the Weibull cure-mixture model, but the difference was unremarkable until late in the trial when evidence for a cure became clear. Nonparametric predictions often gave undefined predictions or infinite prediction intervals, particularly at early stages of the trial. Simulations suggest that cure modeling can yield better-calibrated prediction intervals when there is a cured component, or the appearance of a cured component, but at a substantial cost in the average width of the intervals.

Keywords: Bayesian bootstrap; Enrollment model; Event-based trial; Interim analysis; Weibull distribution.

Figure 1

Kaplan-Meier curves in RTOG 0129: SFX = standard-fractionation radiotherapy alone; AFX = accelerated-fractionation radiotherapy plus concurrent cisplatin-based chemotherapy.

Figure 2

Survival curves for generating the simulation data.

Figure 3

Number of subjects enrolled in each month (30-day interval) during the accrual period.

Figure 4

Number of deaths in each month (30-day interval) during the trial.

Figure 5

Log-scale KM and fitted survival curves from the standard and cure-mixture Weibull models in the AFX arm. Curves for the SFX arm were similar.

Figure 6

Prediction of the 103rd death using NP, standard Weibull and Weibull cure-mixture models. The horizontal dashed line is the date of occurrence of the 103rd death.

Figure 7

Prediction of the 206th death using NP, standard Weibull and Weibull cure-mixture models. The horizontal dashed line is the date of occurrence of the 206th death.

Figure 8

Prediction of the 303rd death using NP, standard Weibull and Weibull cure-mixture models. The horizontal dashed line is the date of occurrence of the 303rd death.

Figure 9

Predicted treatment effect from NP, standard Weibull and Weibull cure-mixture models after the occurrence of the 206th death.

Figure 10

Predictive power from the NP, standard Weibull and Weibull cure-mixture models, by study month.