Epithelial-Mesenchymal Transition in Metastatic Cancer Cell Populations Affects Tumor Dormancy in a Simple Mathematical Model

Abstract

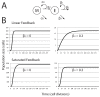
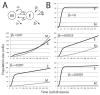
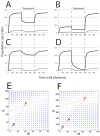
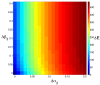
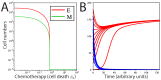
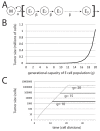
Signaling from the c-Met receptor tyrosine kinase is associated with progression and metastasis of epithelial tumors. c-Met, the receptor for hepatocyte growth factor, triggers epithelial-mesenchymal transition (EMT) of cultured cells, which is thought to drive migration of tumor cells and confer on them critical stem cell properties. Here, we employ mathematical modeling to better understand how EMT affects population dynamics in metastatic tumors. We find that without intervention, micrometastatic tumors reach a steady-state population. While the rates of proliferation, senescence and death only have subtle effects on the steady state, changes in the frequency of EMT dramatically alter population dynamics towards exponential growth. We also find that therapies targeting cell proliferation or cell death are markedly more successful when combined with one that prevents EMT, though such therapies do little when used alone. Stochastic modeling reveals the probability of tumor recurrence from small numbers of residual differentiated tumor cells. EMT events in metastatic tumors provide a plausible mechanism by which clinically detectable tumors can arise from dormant micrometastatic tumors. Modeling the dynamics of this process demonstrates the benefit of a treatment that eradicates tumor cells and reduces the rate of EMT simultaneously.

Keywords: cancer growth; chemotherapy; mathematical modeling; metastasis.

Figure 1

Tumor population dynamics in models of cancers derived from pioneering stem cells. (A) Diagrammatic description of the basic model with M (mesenchymal cells), E (epithelial cells) and their rate parameters; (B) trajectories for M (grey lines) and E (black lines), for the two model variations and two different values of ${\beta }_3$ (senescence of E).

Figure 2

Effect of EMT on the size of metastatic tumors. (A) Modified model diagram, including EMT; (B) each plot shows the trajectories of M and E for different values of ${\beta }_4$ (rate of EMT). As ${\beta }_4$ is increased, the dynamics change from close-to-equilibrium to exponential growth, where eventually, the size of M will overtake E.

Figure 3

Population dynamics in response to chemotherapy. Modeling chemotherapeutic treatment and recurrence; tumor population dynamics before, during and after a treatment regime (denoted by the dashed vertical lines). (A) Treatment consisting of an agent that increased cell death (${\beta }_3$) in the E cell population. At the end of treatment, ${\beta }_3$ returns to its pre-treatment level; (B) The E cell population acquires resistance mutations following treatment (${\beta }_3$ is lower than before treatment); (C) Treatment consisting of an agent that prevents EMT; (D) Treatment consisting of both ${\beta }_3$ reduction and EMT prevention in combined therapy. In (C) and (D), recovery was to original pre-treatment parameter values; (E) The phase plane plot shows the behavior of the system around the fixed Point A (pre-treatment parameter values) and nullclines. Point B marks the system state after treatment; (F) Phase plane plot around the fixed Point C; parameter values after E cells have acquired mutations. In both (E) and (F), the fixed points shown are the only stable fixed points for the system in this state.

Figure 4

Model sensitivity to changes in cell death. We study the effect of increasing the cell death rate of M (${\alpha }_3$) and E (${\beta }_3$) simultaneously. The output is colored by the extent to which the steady state for E is shifted ($\Delta E$). Increasing the rate of M cell death has a much more dramatic effect than increasing the rate of E cell death alone.

Figure 5

Transition from tumor to tumor-free state by induction of cell death. (A) Theoretical dose response curve of stable solutions of E and M as ${\beta }_3$ is varied; (B) solution curves of E at two different rates of cell death (by chemotherapy) with different initial numbers of cells. Red curves represent the solution of E for ${\beta }_3<{\beta }^{*}$; blue curves represent the solution of E for ${\beta }_3>{\beta }^{*}$.

Figure 6

Generational capacity affects dormant tumor steady-state population sizes in a stochastic model. (A) The diagram represents the basic model, where mesenchymal stem cells M divide asymmetrically to generate differentiated epithelial cells E with a generational capacity (g) that measures the number of possible cell divisions that these cells can undergo prior to senescence; (B) steady-state population of tumors derived from a single pioneering M cell with varying g; (C) steady-state population sizes over time for tumors derived from a single M cell.

Figure 7

EMT in a stochastic model of dormant tumor recurrence. (A) The fraction of tumors in which EMT events occur with a fixed generational capacity of 18 and for different probabilities of EMT; (B) the fraction of tumors in which EMT events occur with a varied generational capacity and fixed probability of EMT; (C) the fraction of tumors exhibiting specific numbers of EMT events as generational capacity is altered; (D) the fraction of tumors exhibiting occurrences of EMT over time, for three different generational capacities; (E) the fraction of tumors in which EMT events occur with a varied generational capacity of 18 and fixed probability of EMT. In (A–C), tumors were initiated from a single precursor M cell; while in (D), tumors were started from a population of 100 E cells. The probability of EMT in (B–E) was set at ${10}^{-7}$.