Analytical Derivation of Nonlinear Spectral Effects and 1/f Scaling Artifact in Signal Processing of Real-World Data
- PMID: 28562224
- PMCID: PMC5555851
- DOI: 10.1162/NECO_a_00979
Analytical Derivation of Nonlinear Spectral Effects and 1/f Scaling Artifact in Signal Processing of Real-World Data
Abstract
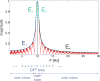
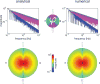
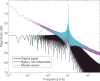
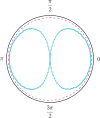
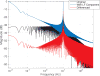
In estimating the frequency spectrum of real-world time series data, we must violate the assumption of infinite-length, orthogonal components in the Fourier basis. While it is widely known that care must be taken with discretely sampled data to avoid aliasing of high frequencies, less attention is given to the influence of low frequencies with period below the sampling time window. Here, we derive an analytic expression for the side-lobe attenuation of signal components in the frequency domain representation. This expression allows us to detail the influence of individual frequency components throughout the spectrum. The first consequence is that the presence of low-frequency components introduces a 1/f[Formula: see text] component across the power spectrum, with a scaling exponent of [Formula: see text]. This scaling artifact could be composed of diffuse low-frequency components, which can render it difficult to detect a priori. Further, treatment of the signal with standard digital signal processing techniques cannot easily remove this scaling component. While several theoretical models have been introduced to explain the ubiquitous 1/f[Formula: see text] scaling component in neuroscientific data, we conjecture here that some experimental observations could be the result of such data analysis procedures.
Figures



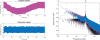

References
-
- Cooley J, Lewis P, Welch P. The finite Fourier transform. IEEE Transactions on Audio and Electroacoustics. 1969;17(2):77–85.
-
- Erdélyi A, editor. Tables of integral transforms. Vol. 1. New York: McGraw-Hill; 1954.
-
- Fourier J. Thïéorie analytique de la chaleur. Chez Firmin Didot; 1822.
-
- Goertzel G. An algorithm for the evaluation of finite trigonometric series. American Mathematical Monthly. 1958;65(1):34–35.
-
- Harris FJ. On the use of windows for harmonic analysis with the discrete Fourier transform. Proceedings of the IEEE. 1978;66(1):51–83.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

