Experimental discrimination of ion stopping models near the Bragg peak in highly ionized matter
- PMID: 28569766
- PMCID: PMC5461488
- DOI: 10.1038/ncomms15693
Experimental discrimination of ion stopping models near the Bragg peak in highly ionized matter
Abstract
The energy deposition of ions in dense plasmas is a key process in inertial confinement fusion that determines the α-particle heating expected to trigger a burn wave in the hydrogen pellet and resulting in high thermonuclear gain. However, measurements of ion stopping in plasmas are scarce and mostly restricted to high ion velocities where theory agrees with the data. Here, we report experimental data at low projectile velocities near the Bragg peak, where the stopping force reaches its maximum. This parameter range features the largest theoretical uncertainties and conclusive data are missing until today. The precision of our measurements, combined with a reliable knowledge of the plasma parameters, allows to disprove several standard models for the stopping power for beam velocities typically encountered in inertial fusion. On the other hand, our data support theories that include a detailed treatment of strong ion-electron collisions.
Conflict of interest statement
The authors declare no competing financial interests.
Figures

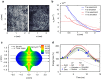
 ≈3.1. The data are compared with the predictions of the LP and the TM stopping-power models applying a Monte-Carlo description as well as the Gus'kov and the Kreussler models for the effective projectile charge state. The energy loss is normalized to its value in the solid target (100%), as well as the plasma areal density (ρR). The error bars correspond to one s.d. (1σ) of the uncertainty in the time shifts of the signals obtained from the TOF measurements.
≈3.1. The data are compared with the predictions of the LP and the TM stopping-power models applying a Monte-Carlo description as well as the Gus'kov and the Kreussler models for the effective projectile charge state. The energy loss is normalized to its value in the solid target (100%), as well as the plasma areal density (ρR). The error bars correspond to one s.d. (1σ) of the uncertainty in the time shifts of the signals obtained from the TOF measurements.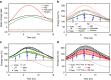
 =ne/2 and temperatures
=ne/2 and temperatures  =Te−40 eV (LP max; TM max) as well as densities
=Te−40 eV (LP max; TM max) as well as densities  =2 ne and temperatures
=2 ne and temperatures  =Te+40 eV (LP min; TM min), respectively. The shaded areas thus illustrate the maximum error in the energy-loss calculation due to uncertainties in the plasma parameters. Due to time averaging over the 5.5 ns bunch, the beam charge state in a as well as the energy loss in (b–d) for t=0 ns, are already larger than their respective values in the solid target. The error bars on the energy loss correspond to one s.d. (1σ) of the uncertainty in the time shifts in the detector signals.
=Te+40 eV (LP min; TM min), respectively. The shaded areas thus illustrate the maximum error in the energy-loss calculation due to uncertainties in the plasma parameters. Due to time averaging over the 5.5 ns bunch, the beam charge state in a as well as the energy loss in (b–d) for t=0 ns, are already larger than their respective values in the solid target. The error bars on the energy loss correspond to one s.d. (1σ) of the uncertainty in the time shifts in the detector signals.
References
-
- Hurricane O. A. et al.. Inertially confined fusion plasmas dominated by alpha-particle self-heating. Nat. Phys. 12, 800–806 (2016).
-
- Callahan-Miller D. A. & Tabak M. Progress in target physics and design for heavy ion fusion. Phys. Plasmas 7, 2083–2091 (2000).
-
- Fernández J. C. et al.. Fast ignition with laser-driven proton and ion beams. Nucl. Fusion 54, 054006 (2014).
-
- Deutsch C. et al.. Ion stopping in dense plasma target for high energy density physics. Open Plasma Phys. J. 3, 88–115 (2010).
-
- Maynard G. & Deutsch C. Born random phase approximation for ion stopping in an arbitrarily degenerate electron fluid. J. Phys. 46, 1113–1122 (1985).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

