Three-Dimensional Anisotropic Metamaterials as Triaxial Optical Inclinometers
- PMID: 28578422
- PMCID: PMC5457403
- DOI: 10.1038/s41598-017-02865-z
Three-Dimensional Anisotropic Metamaterials as Triaxial Optical Inclinometers
Abstract
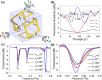
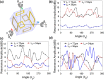
Split-ring resonators (SRRs) present an attractive avenue for the development of micro/nano scale inclinometers for applications like medical microbots, military hardware, and nanosatellite systems. However, the 180° isotropy of their two-dimensional structure presents a major hurdle. In this paper, we present the design of a three-dimensional (3D) anisotropic SRR functioning as a microscale inclinometer enabling it to remotely sense rotations from 0° to 360° along all three axes (X, Y, and Z), by employing the geometric property of a 3D structure. The completely polymeric composition of the cubic structure renders it transparent to the Terahertz (THz) light, providing a transmission response of the tilted SRRs patterned on its surface that is free of any distortion, coupling, and does not converge to a single point for two different angular positions. Fabrication, simulation, and measurement data have been presented to demonstrate the superior performance of the 3D micro devices.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures




Similar articles
-
Fabrication of Nanopillar-Based Split Ring Resonators for Displacement Current Mediated Resonances in Terahertz Metamaterials.J Vis Exp. 2017 Mar 23;(121):55289. doi: 10.3791/55289. J Vis Exp. 2017. PMID: 28362392 Free PMC article.
-
Controlling bi-anisotropy in infrared metamaterials using three-dimensional split-ring-resonators for purely magnetic resonance.Sci Rep. 2017 Jul 27;7(1):6726. doi: 10.1038/s41598-017-07026-w. Sci Rep. 2017. PMID: 28751761 Free PMC article.
-
Bi-anisotropic Fano resonance in three-dimensional metamaterials.Sci Rep. 2018 Jun 13;8(1):9012. doi: 10.1038/s41598-018-27404-2. Sci Rep. 2018. PMID: 29899415 Free PMC article.
-
Resonance control of mid-infrared metamaterials using arrays of split-ring resonator pairs.Nanotechnology. 2016 Feb 5;27(5):055303. doi: 10.1088/0957-4484/27/5/055303. Epub 2016 Jan 11. Nanotechnology. 2016. PMID: 26751676
-
Small-Scale Biological and Artificial Multidimensional Sensors for 3D Sensing.Small. 2018 Aug;14(35):e1801145. doi: 10.1002/smll.201801145. Epub 2018 Jul 30. Small. 2018. PMID: 30062866 Review.
References
-
- Alves, F., Dias, R. A., Cabral, J. & Rocha, L. A. In Autonomous and Intelligent Systems 26–33 (Springer, 2012).
-
- Zou X, Thiruvenkatanathan P, Seshia AA. A high-resolution micro-electro-mechanical resonant tilt sensor. Sens. Actuators, A. 2014;220:168–177. doi: 10.1016/j.sna.2014.10.004. - DOI
-
- Chang C, Tsai M, Liu Y, Sun C, Fang W. Pick-and-place process for sensitivity improvement of the capacitive type CMOS MEMS 2-axis tilt sensor. J. Micromech. Microeng. 2013;23:095029. doi: 10.1088/0960-1317/23/9/095029. - DOI
-
- Bilham R. Borehole inclinometer monument for millimeter horizontal geodetic control accuracy. Geophys. Res. Lett. 1993;20:2159–2162. doi: 10.1029/93GL02636. - DOI
-
- Kottapalli VA, et al. Proc. SPIE. 2003. Two-tiered wireless sensor network architecture for structural health monitoring; pp. 8–19.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

