Cascaded spintronic logic with low-dimensional carbon
- PMID: 28580930
- PMCID: PMC5465351
- DOI: 10.1038/ncomms15635
Cascaded spintronic logic with low-dimensional carbon
Abstract
Remarkable breakthroughs have established the functionality of graphene and carbon nanotube transistors as replacements to silicon in conventional computing structures, and numerous spintronic logic gates have been presented. However, an efficient cascaded logic structure that exploits electron spin has not yet been demonstrated. In this work, we introduce and analyse a cascaded spintronic computing system composed solely of low-dimensional carbon materials. We propose a spintronic switch based on the recent discovery of negative magnetoresistance in graphene nanoribbons, and demonstrate its feasibility through tight-binding calculations of the band structure. Covalently connected carbon nanotubes create magnetic fields through graphene nanoribbons, cascading logic gates through incoherent spintronic switching. The exceptional material properties of carbon materials permit Terahertz operation and two orders of magnitude decrease in power-delay product compared to cutting-edge microprocessors. We hope to inspire the fabrication of these cascaded logic circuits to stimulate a transformative generation of energy-efficient computing.
Conflict of interest statement
The authors declare no competing financial interests.
Figures

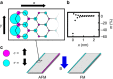

 of the AFM state defines the number of available conduction modes as well as the probability for an electron to travel across the device. Thus, for EF values within the bandgap, the GNR conductance switches when the global ordering switches between the FM and AFM states. (f) A typical switching event, where the GNR conductance increases by G0 when the CNT current overcomes the critical switching current IC.
of the AFM state defines the number of available conduction modes as well as the probability for an electron to travel across the device. Thus, for EF values within the bandgap, the GNR conductance switches when the global ordering switches between the FM and AFM states. (f) A typical switching event, where the GNR conductance increases by G0 when the CNT current overcomes the critical switching current IC.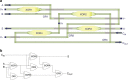
 ⊕B. The output of XOR1 flows through a CNT that functions as an input to XOR2 and XOR3 before reaching the wired-OR gate OR2, which merges currents to compute CINV(A⊕B). This current controls XOR4 and terminates at V−. The other currents operate similarly, computing the one-bit addition function with output current signals S and COUT. (b) In the symbolic circuit diagram shown here with conventional symbols, the output of XOR1 is used as an input to OR2 and XOR3 along with CIN. The full adder S output is computed as S=CINV⊕(A⊕B). OR2 outputs CINV(A⊕B), which is used along with S as an input to XOR4 to compute (CINV(A⊕B))⊕(CIN⊕(A⊕B)). This output of XOR4 is equivalent to (A∧CIN)V(B∧CIN). OR3 takes this signal as an input along with the output of XOR2, which is equal to A∧B, to compute COUT=(A∧B)V(A∧CIN)V(B∧CIN). As the wired-OR gates simply sum the currents and have no significant delay, the total propagation time is that of three XOR gates, determined by the XOR1–XOR3–XOR4 worst-case path.
⊕B. The output of XOR1 flows through a CNT that functions as an input to XOR2 and XOR3 before reaching the wired-OR gate OR2, which merges currents to compute CINV(A⊕B). This current controls XOR4 and terminates at V−. The other currents operate similarly, computing the one-bit addition function with output current signals S and COUT. (b) In the symbolic circuit diagram shown here with conventional symbols, the output of XOR1 is used as an input to OR2 and XOR3 along with CIN. The full adder S output is computed as S=CINV⊕(A⊕B). OR2 outputs CINV(A⊕B), which is used along with S as an input to XOR4 to compute (CINV(A⊕B))⊕(CIN⊕(A⊕B)). This output of XOR4 is equivalent to (A∧CIN)V(B∧CIN). OR3 takes this signal as an input along with the output of XOR2, which is equal to A∧B, to compute COUT=(A∧B)V(A∧CIN)V(B∧CIN). As the wired-OR gates simply sum the currents and have no significant delay, the total propagation time is that of three XOR gates, determined by the XOR1–XOR3–XOR4 worst-case path.

References
-
- Ney A., Pampuch C., Koch R. & Ploog K. H. Programmable computing with a single magnetoresistive element. Nature 425, 485–487 (2003). - PubMed
-
- Allwood D. A. et al.. Magnetic domain-wall logic. Science 309, 1688–1692 (2005). - PubMed
-
- Awschalom D. & Flatte M. Challenges for semiconductor spintronics. Nat. Phys. 3, 153–159 (2007).
-
- Dery H., Dalal P., Cywiński Ł. & Sham L. J. Spin-based logic in semiconductors for reconfigurable large-scale circuits. Nature 447, 573–576 (2007). - PubMed
-
- Behin-Aein B., Datta D., Salahuddin S. & Datta S. Proposal for an all-spin logic device with built-in memory. Nat. Nanotechnol. 5, 266–270 (2010). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

