Adaptive self-organization of Bali's ancient rice terraces

Abstract

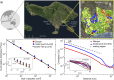
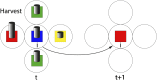
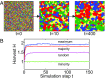
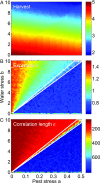
Spatial patterning often occurs in ecosystems as a result of a self-organizing process caused by feedback between organisms and the physical environment. Here, we show that the spatial patterns observable in centuries-old Balinese rice terraces are also created by feedback between farmers' decisions and the ecology of the paddies, which triggers a transition from local to global-scale control of water shortages and rice pests. We propose an evolutionary game, based on local farmers' decisions that predicts specific power laws in spatial patterning that are also seen in a multispectral image analysis of Balinese rice terraces. The model shows how feedbacks between human decisions and ecosystem processes can evolve toward an optimal state in which total harvests are maximized and the system approaches Pareto optimality. It helps explain how multiscale cooperation from the community to the watershed scale could persist for centuries, and why the disruption of this self-organizing system by the Green Revolution caused chaos in irrigation and devastating losses from pests. The model shows that adaptation in a coupled human-natural system can trigger self-organized criticality (SOC). In previous exogenously driven SOC models, adaptation plays no role, and no optimization occurs. In contrast, adaptive SOC is a self-organizing process where local adaptations drive the system toward local and global optima.

Keywords: Pareto optimality; criticality; evolutionary games; irrigation; self-organization.

Fig. 1.

(A) Location of study sites: six randomly selected rice-growing regions of Bali. Photosynthetic activity was analyzed using multispectral and panchromatic satellite images to classify four stages of rice growth in the terraces, which appear as differently colored patches. (B) Image analysis of rice growth (indicating synchronized irrigation schedules in the region of Gianyar). The four colors of the patches indicate the four stages: growing rice (yellow), harvest (green), flooded (red), drained (blue). (C) Cumulative distribution of the patch sizes $P(>s)$ for Gianyar (red circles) and for our model results (blue squares). (Inset) All 13 observations at the six regions, indicating power-law behavior, with an exponent around $\alpha \approx 1$. (D) Correlation functions $C(d)$ of the image (planting regions only) as a function of distance for Gianyar (red) and the model (blue). The slow decay (power law) indicates long-range correlations, or “system-wide connectivity” of patches. (Inset) All 13 observations. See SI Appendix for details.

Fig. 2.

Update rule for farmer $i$. Colors denote irrigation schedules. For example, green might signify planting in January, and blue might signify planting in March. At time $t+1$, farmer $i$ compares his harvest with those of his four closest neighbors at time $t$. Because the red schedule produced the best harvests, he adopts it for the next cycle. This update corresponds to step iii in the model.

Fig. 3.

(A) Evolution of the irrigation schedules from an initial random configuration at $t=0$ to $t=10$, whereupon patch sizes become power-law distributed. At $t=400$, the irrigation patterns have changed very little and approach a long-lived steady state distribution (see SI Appendix). (B) Effect of decision rules on harvests. For the “maximum” rule (step iii, where farmers choose the best harvest in their neighborhood), average harvests rapidly increase as patch distributions shift to the power-law distribution (blue line). A similar rapid increase occurs for the “majority” update strategy, where farmers copy the schedule of the majority (red). To copy a random neighbor’s irrigation schedule is the “random” strategy (pink) that leads to inferior harvests. Extending this logic, when farmers update according to the minority of their neighbors, harvests do not improve. The maximum possible harvest is $H=H_0=5$ in the absence of pest or water stress. In the simulation shown, both pest and water stress are strongly present, $a=0.5$ and $b=9.6$.

Fig. 4.

Effects of pest and water stress: model results as a function of parameters $a$ (pests) and $b$ (water). (A) Average harvests. The maximum possible harvest $H_0$ occurs when $a=b=0$. (B) Power-law exponent $\alpha$ of the cumulative patch size distribution. The parameter region that matches the observed slopes from the satellite imagery (SI Appendix, Table S2) is indicated by the white line. (C) Correlation length $\epsilon$. The parameter region that matches the observed slopes from the satellite imagery (SI Appendix, Table S2) is found around the line where $b/a\approx 20$, which is indicated with the white line. Further computations show the same critical behavior at $b/a\approx 14$ when $m=0.2$, or at $b/a\approx 24$ for $m=0.05$ (see SI Appendix, Fig. S2). Thus, the emergence of critical behavior does not depend simply on $a$ and $b$ but also on the constant $m$ in the denominator of pest stress. In conclusion, taking results from exponents and correlation lengths, the parameter region that is compatible with observations is $b/a\approx 20$. Simulations were performed with $L=100$, $r=2$, $f=0.05$, and $N=4$.