Experimental Evolution with Caenorhabditis Nematodes
- PMID: 28592504
- PMCID: PMC5499180
- DOI: 10.1534/genetics.115.186288
Experimental Evolution with Caenorhabditis Nematodes
Abstract
The hermaphroditic nematode Caenorhabditis elegans has been one of the primary model systems in biology since the 1970s, but only within the last two decades has this nematode also become a useful model for experimental evolution. Here, we outline the goals and major foci of experimental evolution with C. elegans and related species, such as C. briggsae and C. remanei, by discussing the principles of experimental design, and highlighting the strengths and limitations of Caenorhabditis as model systems. We then review three exemplars of Caenorhabditis experimental evolution studies, underlining representative evolution experiments that have addressed the: (1) maintenance of genetic variation; (2) role of natural selection during transitions from outcrossing to selfing, as well as the maintenance of mixed breeding modes during evolution; and (3) evolution of phenotypic plasticity and its role in adaptation to variable environments, including host-pathogen coevolution. We conclude by suggesting some future directions for which experimental evolution with Caenorhabditis would be particularly informative.
Keywords: C. briggsae; C. elegans; C. remanei; WormBook; adaptation; domestication; experimental design; laboratory selection experiments; mutation accumulation; reproduction systems; self-fertilization; standing genetic variation.
Copyright © 2017 Teotónio et al.
Figures
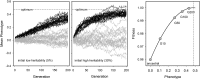
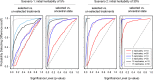
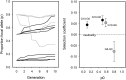
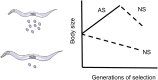


References
-
- Agrawal A., Lively C. M., 2002. Infection genetics: gene-for-gene vs. matching-alleles models and all points in between. Evol. Ecol. Res. 4: 79–90.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

