Network dynamics of social influence in the wisdom of crowds
- PMID: 28607070
- PMCID: PMC5495222
- DOI: 10.1073/pnas.1615978114
Network dynamics of social influence in the wisdom of crowds
Abstract
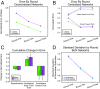
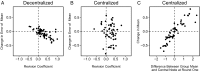
A longstanding problem in the social, biological, and computational sciences is to determine how groups of distributed individuals can form intelligent collective judgments. Since Galton's discovery of the "wisdom of crowds" [Galton F (1907) Nature 75:450-451], theories of collective intelligence have suggested that the accuracy of group judgments requires individuals to be either independent, with uncorrelated beliefs, or diverse, with negatively correlated beliefs [Page S (2008) The Difference: How the Power of Diversity Creates Better Groups, Firms, Schools, and Societies]. Previous experimental studies have supported this view by arguing that social influence undermines the wisdom of crowds. These results showed that individuals' estimates became more similar when subjects observed each other's beliefs, thereby reducing diversity without a corresponding increase in group accuracy [Lorenz J, Rauhut H, Schweitzer F, Helbing D (2011) Proc Natl Acad Sci USA 108:9020-9025]. By contrast, we show general network conditions under which social influence improves the accuracy of group estimates, even as individual beliefs become more similar. We present theoretical predictions and experimental results showing that, in decentralized communication networks, group estimates become reliably more accurate as a result of information exchange. We further show that the dynamics of group accuracy change with network structure. In centralized networks, where the influence of central individuals dominates the collective estimation process, group estimates become more likely to increase in error.
Keywords: collective intelligence; experimental social science; social learning; social networks; wisdom of crowds.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

Comment in
-
Reply to Bruggeman: Learning is robust to noise in decentralized networks.Proc Natl Acad Sci U S A. 2017 Oct 31;114(44):E9184. doi: 10.1073/pnas.1714427114. Epub 2017 Oct 26. Proc Natl Acad Sci U S A. 2017. PMID: 29078400 Free PMC article. No abstract available.
Similar articles
-
Adaptive social networks promote the wisdom of crowds.Proc Natl Acad Sci U S A. 2020 May 26;117(21):11379-11386. doi: 10.1073/pnas.1917687117. Epub 2020 May 11. Proc Natl Acad Sci U S A. 2020. PMID: 32393632 Free PMC article.
-
The wisdom of partisan crowds.Proc Natl Acad Sci U S A. 2019 May 28;116(22):10717-10722. doi: 10.1073/pnas.1817195116. Epub 2019 May 13. Proc Natl Acad Sci U S A. 2019. PMID: 31085635 Free PMC article.
-
How social influence can undermine the wisdom of crowd effect.Proc Natl Acad Sci U S A. 2011 May 31;108(22):9020-5. doi: 10.1073/pnas.1008636108. Epub 2011 May 16. Proc Natl Acad Sci U S A. 2011. PMID: 21576485 Free PMC article.
-
The network science of collective intelligence.Trends Cogn Sci. 2022 Nov;26(11):923-941. doi: 10.1016/j.tics.2022.08.009. Epub 2022 Sep 27. Trends Cogn Sci. 2022. PMID: 36180361 Review.
-
How large language models can reshape collective intelligence.Nat Hum Behav. 2024 Sep;8(9):1643-1655. doi: 10.1038/s41562-024-01959-9. Epub 2024 Sep 20. Nat Hum Behav. 2024. PMID: 39304760 Review.
Cited by
-
Individual and collective learning in groups facing danger.Sci Rep. 2022 Apr 13;12(1):6210. doi: 10.1038/s41598-022-10255-3. Sci Rep. 2022. PMID: 35418611 Free PMC article.
-
Discussions of Asperger Syndrome on Social Media: Content and Sentiment Analysis on Twitter.JMIR Form Res. 2022 Mar 7;6(3):e32752. doi: 10.2196/32752. JMIR Form Res. 2022. PMID: 35254265 Free PMC article.
-
Sensing Enhancement on Social Networks: The Role of Network Topology.Entropy (Basel). 2022 May 22;24(5):738. doi: 10.3390/e24050738. Entropy (Basel). 2022. PMID: 35626621 Free PMC article.
-
Social learning and partisan bias in the interpretation of climate trends.Proc Natl Acad Sci U S A. 2018 Sep 25;115(39):9714-9719. doi: 10.1073/pnas.1722664115. Epub 2018 Sep 4. Proc Natl Acad Sci U S A. 2018. PMID: 30181271 Free PMC article.
-
Quantifying the vulnerabilities of the online public square to adversarial manipulation tactics.PNAS Nexus. 2024 Jun 29;3(7):pgae258. doi: 10.1093/pnasnexus/pgae258. eCollection 2024 Jul. PNAS Nexus. 2024. PMID: 38994499 Free PMC article.
References
-
- Galton F. Vox populi (The wisdom of crowds) Nature. 1907;75:450–51.
-
- Sunstein CR. Infotopia: How Many Minds Produce Knowledge. Oxford Univ Press; Oxford: 2006.
-
- Wolfers J, Zitzewitz E. Prediction markets. J Econ Perspect. 2004;18:107–126.
-
- Kelley EK, Tetlock PC. How wise are crowds? Insights from retail orders and stock returns. J Finance. 2013;68(3):1229–1265.
-
- Nofer M, Hinz O. Are crowds on the internet wiser than experts? The case of a stock prediction community. J Bus Econ. 2014;84(3):303–338.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

