Robust transmission of rate coding in the inhibitory Purkinje cell to cerebellar nuclei pathway in awake mice
- PMID: 28617798
- PMCID: PMC5491311
- DOI: 10.1371/journal.pcbi.1005578
Robust transmission of rate coding in the inhibitory Purkinje cell to cerebellar nuclei pathway in awake mice
Abstract
Neural coding through inhibitory projection pathways remains poorly understood. We analyze the transmission properties of the Purkinje cell (PC) to cerebellar nucleus (CN) pathway in a modeling study using a data set recorded in awake mice containing respiratory rate modulation. We find that inhibitory transmission from tonically active PCs can transmit a behavioral rate code with high fidelity. We parameterized the required population code in PC activity and determined that 20% of PC inputs to a full compartmental CN neuron model need to be rate-comodulated for transmission of a rate code. Rate covariance in PC inputs also accounts for the high coefficient of variation in CN spike trains, while the balance between excitation and inhibition determines spike rate and local spike train variability. Overall, our modeling study can fully account for observed spike train properties of cerebellar output in awake mice, and strongly supports rate coding in the cerebellum.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

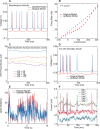


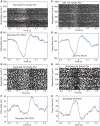
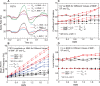

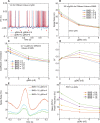
References
-
- Eliasmith C, Stewart TC, Choo X, Bekolay T, DeWolf T, et al. (2012) A Large-Scale Model of the Functioning Brain. Science 338: 1202–1205. doi: 10.1126/science.1225266 - DOI - PubMed
-
- Walter JT, Khodakhah K (2006) The linear computational algorithm of cerebellar Purkinje cells. Journal of Neuroscience 26: 12861–12872. doi: 10.1523/JNEUROSCI.4507-05.2006 - DOI - PMC - PubMed
-
- Walter JT, Khodakhah K (2009) The advantages of linear information processing for cerebellar computation. Proceedings of the National Academy of Sciences of the United States of America 106: 4471–4476. doi: 10.1073/pnas.0812348106 - DOI - PMC - PubMed
-
- Cao Y, Maran SK, Dhamala M, Jaeger D, Heck DH (2012) Behavior-Related Pauses in Simple-Spike Activity of Mouse Purkinje Cells Are Linked to Spike Rate Modulation. Journal of Neuroscience 32: 8678–8685. doi: 10.1523/JNEUROSCI.4969-11.2012 - DOI - PMC - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

