Simulating tactile signals from the whole hand with millisecond precision
- PMID: 28652360
- PMCID: PMC5514748
- DOI: 10.1073/pnas.1704856114
Simulating tactile signals from the whole hand with millisecond precision
Abstract
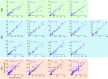
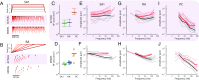
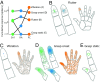
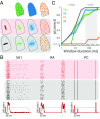
When we grasp and manipulate an object, populations of tactile nerve fibers become activated and convey information about the shape, size, and texture of the object and its motion across the skin. The response properties of tactile fibers have been extensively characterized in single-unit recordings, yielding important insights into how individual fibers encode tactile information. A recurring finding in this extensive body of work is that stimulus information is distributed over many fibers. However, our understanding of population-level representations remains primitive. To fill this gap, we have developed a model to simulate the responses of all tactile fibers innervating the glabrous skin of the hand to any spatiotemporal stimulus applied to the skin. The model first reconstructs the stresses experienced by mechanoreceptors when the skin is deformed and then simulates the spiking response that would be produced in the nerve fiber innervating that receptor. By simulating skin deformations across the palmar surface of the hand and tiling it with receptors at their known densities, we reconstruct the responses of entire populations of nerve fibers. We show that the simulated responses closely match their measured counterparts, down to the precise timing of the evoked spikes, across a wide variety of experimental conditions sampled from the literature. We then conduct three virtual experiments to illustrate how the simulation can provide powerful insights into population coding in touch. Finally, we discuss how the model provides a means to establish naturalistic artificial touch in bionic hands.
Keywords: computational model; mechanoreceptor; skin mechanics; somatosensory periphery; tactile afferent.
Conflict of interest statement
The authors declare no conflict of interest.
Figures








References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

