Morphological Plant Modeling: Unleashing Geometric and Topological Potential within the Plant Sciences
- PMID: 28659934
- PMCID: PMC5465304
- DOI: 10.3389/fpls.2017.00900
Morphological Plant Modeling: Unleashing Geometric and Topological Potential within the Plant Sciences
Abstract
The geometries and topologies of leaves, flowers, roots, shoots, and their arrangements have fascinated plant biologists and mathematicians alike. As such, plant morphology is inherently mathematical in that it describes plant form and architecture with geometrical and topological techniques. Gaining an understanding of how to modify plant morphology, through molecular biology and breeding, aided by a mathematical perspective, is critical to improving agriculture, and the monitoring of ecosystems is vital to modeling a future with fewer natural resources. In this white paper, we begin with an overview in quantifying the form of plants and mathematical models of patterning in plants. We then explore the fundamental challenges that remain unanswered concerning plant morphology, from the barriers preventing the prediction of phenotype from genotype to modeling the movement of leaves in air streams. We end with a discussion concerning the education of plant morphology synthesizing biological and mathematical approaches and ways to facilitate research advances through outreach, cross-disciplinary training, and open science. Unleashing the potential of geometric and topological approaches in the plant sciences promises to transform our understanding of both plants and mathematics.
Keywords: mathematics; modeling; morphology; plant biology; plant science; topology.
Figures
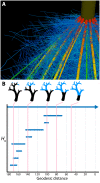
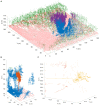

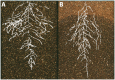

 , and
, and  are the spring constant, current length, and rest length for wall a. KP is a constant and SA is the size of cell A. Δt is time step. Shown is a simulation of cell network growth. (B) Reaction diffusion model of the shoot apical meristem for WUSCHEL and CLAVATA interactions (Fujita et al., 2011). u = WUS, v = CLV, i = cell index, Φ is a sigmoid function. E, B, AS, Ad, C, D, um, Du, Dv are positive constants. Shown are the distributions of WUS and CLV levels within a dynamic cell network. Images provided by DB (Virginia Tech).
are the spring constant, current length, and rest length for wall a. KP is a constant and SA is the size of cell A. Δt is time step. Shown is a simulation of cell network growth. (B) Reaction diffusion model of the shoot apical meristem for WUSCHEL and CLAVATA interactions (Fujita et al., 2011). u = WUS, v = CLV, i = cell index, Φ is a sigmoid function. E, B, AS, Ad, C, D, um, Du, Dv are positive constants. Shown are the distributions of WUS and CLV levels within a dynamic cell network. Images provided by DB (Virginia Tech).

References
-
- Aiteanu F., Klein R. (2014). Hybrid tree reconstruction from inhomogeneous point clouds. Visual Comput. 30 763–771. 10.1007/s00371-014-0977-7 - DOI
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

