The Structured Coalescent and Its Approximations

Abstract

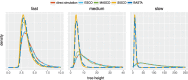
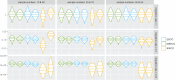
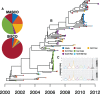
Phylogeographic methods can help reveal the movement of genes between populations of organisms. This has been widely done to quantify pathogen movement between different host populations, the migration history of humans, and the geographic spread of languages or gene flow between species using the location or state of samples alongside sequence data. Phylogenies therefore offer insights into migration processes not available from classic epidemiological or occurrence data alone. Phylogeographic methods have however several known shortcomings. In particular, one of the most widely used methods treats migration the same as mutation, and therefore does not incorporate information about population demography. This may lead to severe biases in estimated migration rates for data sets where sampling is biased across populations. The structured coalescent on the other hand allows us to coherently model the migration and coalescent process, but current implementations struggle with complex data sets due to the need to infer ancestral migration histories. Thus, approximations to the structured coalescent, which integrate over all ancestral migration histories, have been developed. However, the validity and robustness of these approximations remain unclear. We present an exact numerical solution to the structured coalescent that does not require the inference of migration histories. Although this solution is computationally unfeasible for large data sets, it clarifies the assumptions of previously developed approximate methods and allows us to provide an improved approximation to the structured coalescent. We have implemented these methods in BEAST2, and we show how these methods compare under different scenarios.

Keywords: infectious diseases; migration; phylodynamics; phylogenetics; phylogeography; population structure.

Fig. 1.

Comparison of MCMC sampled to simulated tree heights using the different structured coalescent approaches. Sampled tree heights in arbitrary units of time when the rates of migration are fast, that is, in the same order of magnitude as coalescence, when the rates of migration are medium, that is, one order of magnitude lower than coalescence and slow, that is, two orders of magnitude lower than coalescence. The trees were sampled using MCMC for one million iterations, storing every thousandth step, after a burn-in of 20%.

Fig. 2.

Inferred location of the root for different migration rates and structured coalescent approaches. The plot shows the probability of the root being in the blue state (y-axis) depending on the migration rate from blue to brown (x-axis), for the given tree and sampling states. The migration rate from brown to blue was held constant at 0.01. The height of the tree was ∼42 arbitrary units of time and the coalescent rates were 2 (in blue) and 4 (in red).

Fig. 3.

Maximum likelihood estimates of migration rates using the exact structured coalescent and its approximations. Here, we compare simulated migration rates (x-axis) to the maximum likelihood estimates of the migration rate (y-axis), estimated using the exact structured coalescent ESCO and its approximations MASCO and SISCO. The coalescent rates are fixed to the truth, and the migration rates are assumed to be symmetric. The red line indicates where the true values should lie.

Fig. 4.

Inferred asymmetry of migration and coalescent rates. Here we show the inferred median coalescent (upper row) and migration (lower row) rate ratios under different conditions. In the first column, the coalescent rate ratios (x-axis) are varied while the migration rates ratios are kept constant. In the second column, the migration rate ratios (x-axis) are varied, whereas the coalescent rate ratios are kept constant. We simulated a total of 2,000 trees using MASTER with 100 tips from each of the two different states sampled uniformly between times t = 0 and t = 10. Of these trees, 1,000 were simulated with pairwise coalescent rate ratios λ₁/λ₂ from 0.01 to 1, λ₁ + λ₂ = 4 and migration rates in both directions equal to 1. The other 1,000 trees were simulated with migration rate ratios from m₁₂/m₂₁ from 0.01 to 1, m₁₂ + m₂₁ = 2 and pairwise coalescent rates in both states equal to 2, using exponential priors with mean 2 for the coalescent rates and mean 1 for the migration rates. Both coalescent rates and both migration rates are estimated. The red line indicates where the estimates should lie.

Fig. 5.

Inferred migration rates under different sampling conditions. The plot shows the distribution of mean inferred migration rates using ESCO, MASCO, and SISCO. From the left, the first distribution of a color (indicating the different methods) always shows the distribution of mean inferred migration rates from state 1 to state 2. The second distribution from the same color shows the rates from state 2 to 1. From left to right the number of samples from state 1 and state 2 are changed, whereas from top to bottom the true symmetric migration rates are going from 1 to 0.01. The lines within the violin plots indicate the first, second, and third quantiles. The coalescent rates were 2 in both states and the migration rates ranged from 0.01 to 1. The migration rates were always symmetric, that is, the same in both directions. The leaves were sampled uniformly between t = 0 and t = 25. Each simulation was repeated 100 times and each inference was run with 3 parallel MCMC chains, each with different initial values. An exponential prior distribution with the mean $=1$ was used on the migration and coalescent rates.

Fig. 6.

Inference of the root regions of AIV sampled from different places in North America. (A) Maximum clade credibility tree inferred from AIV sequences sampled in different regions of the USA, Canada, and Mexico using MASCO as a population prior. The node heights represent the mean node heights. The tip colors indicate the different sampling regions shown in the legend. (B) Inferred root regions using MASCO (top) and SISCO (bottom). The pie charts show the inferred probability of the root being in either of the different states/regions by MASCO and SISCO. (C) Violin plots of the inferred coalescent rates for the different regions. The black plot distribution is the exponential prior with mean 1. We used this prior for both coalescent and migration rates.

Fig. 7.

Events and configurations on an example tree. Here, we illustrate the possible events and the configurations before and after each event on a simple tree, with time going backwards from present to past. The first two lineages, are both in state blue, that is, the configuration is $(L_1=blue,L_2=blue)$, with lineage 1 being the parent lineage of 1 and 2 after relabeling. After a lineage in state red is sampled, the configuration changes, as given in the figure. A coalescent event in state blue then reduces the number of lineages in state blue to 1. A migration event then causes lineage L₁ to change state from blue to red.