Dynamical models of mutated chronic myelogenous leukemia cells for a post-imatinib treatment scenario: Response to dasatinib or nilotinib therapy

Abstract

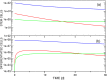
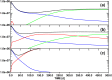
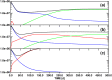
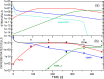
Targeted inhibition of the oncogenic BCR-ABL1 fusion protein using the ABL1 tyrosine kinase inhibitor imatinib has become standard therapy for chronic myelogenous leukemia (CML), with most patients reaching total and durable remission. However, a significant fraction of patients develop resistance, commonly due to mutated ABL1 kinase domains. This motivated development of second-generation drugs with broadened or altered protein kinase selectivity profiles, including dasatinib and nilotinib. Imatinib-resistant patients undergoing treatment with second-line drugs typically develop resistance to them, but dynamic and clonal properties of this response differ. Shared, however, is the observation of clonal competition, reflected in patterns of successive dominance of individual clones. We present three deterministic mathematical models to study the origins of clinically observed dynamics. Each model is a system of coupled first-order differential equations, considering populations of three mutated active stem cell strains and three associated pools of differentiated cells; two models allow for activation of quiescent stem cells. Each approach is distinguished by the way proliferation rates of the primary stem cell reservoir are modulated. Previous studies have concentrated on simulating the response of wild-type leukemic cells to imatinib administration; our focus is on modelling the time dependence of imatinib-resistant clones upon subsequent exposure to dasatinib or nilotinib. Performance of the three computational schemes to reproduce selected CML patient profiles is assessed. While some simple cases can be approximated by a basic design that does not invoke quiescence, others are more complex and require involvement of non-cycling stem cells for reproduction. We implement a new feedback mechanism for regulation of coupling between cycling and non-cycling stem cell reservoirs that depends on total cell populations. A bifurcation landscape analysis is also performed for solutions to the basic ansatz. Computational models reproducing patient data illustrate potential dynamic mechanisms that may guide optimization of therapy of drug resistant CML.

Fig 1. Schematic overview of key characteristics of the computational models developed in Secs. 2.3, 2.4, and 2.5.

All models feature a stem and a differentiated cell compartment. The differentiated cell compartment integrates the three layers of progenitor, differentiated and terminally differentiated cells. In both compartments, normal and wild-type CML cell populations are treated as stable in time over the simulation period, which corresponds to administration of dasatinib or nilotinib, and are not included in the dynamical models. Competition for resources is restricted to three imatinib-resistant clones of cycling stem cells (x_s1(t), x_s2(t), x_s3(t)) and differentiated cells (x_d1(t), x_d2(t), x_d3(t)). The rates of symmetric and asymmetric stem cell division are controlled by the growth functions ζ_i(x_s(t)) defined in Eq (6). Only mutations of the initially dominant clone x_s1(t) into x_s2(t) and x_s3(t) are taken into account, the relevant rate constants are ν₂ and ν₃, respectively. The individual models are distinguished by the way in which stem cells of type mutation 1 are interconverting between the growth environments “quiescent” (x_q1(t)) and “cycling” (x_s1(t)), the characteristic rate constants are ν_q1 and ν_c1. Quiescent stem cells reservoirs for mutations 2 and 3 are not included in the model.

Fig 2. Test simulation of the competition dynamics of three imatinib-resistant stem cell clones (a) and of the associated differentiated cell populations (b) employing model A (Eq (4)).

The focus is on the initial phase of dasatinib treatment, in which an equilibrium between the populations of stem and differentiated cells is established. In panel (b), the time axis corresponds to the interval [0d,30d] of panel Fig 3(a). Accordingly, the threshold setting is θ_s2 = 10.0. The other parameters employed for the simulation are compiled in Table 2. Color scheme: x_s1 / x_d1 (blue), x_s2 / x_d2 (red), x_s3 / x_d3 (green). The ordinate units of panels (a) and (b) are arbitrary and number of cells / ml blood, respectively.

Fig 3. Test simulations of the population dynamics of three imatinib-resistant differentiated cell clones and of the total number of differentiated cells based on model A (Eq (4)).

The panels (a), (b) and (c) correspond to the threshold settings θ_s2 = 10.0, 100.0 and 500.0, respectively. The other parameters employed for the simulations are compiled in Table 2. Color scheme: x_d1 (blue), x_d2 (red), x_d3 (green) and y (black). The ordinate unit is number of cells / ml blood.

Fig 4. Test simulations of the population dynamics of three imatinib-resistant differentiated cell clones and of the total number of differentiated cells based on model B (Eq (7)) with parameters x_q1(0) = 10.0 and ν_q1 = 0.1.

The panels (a), (b) and (c) correspond to the threshold settings θ_s2 = 10.0, 100.0 and 500.0, respectively. The other parameters employed for the simulations are compiled in Table 2. Color scheme: x_d1 (blue), x_d2 (red), x_d3 (green) and y (black). The ordinate unit is number of cells / ml blood.

Fig 5. Results obtained with the same model as Fig 4, except that x_q1(0) = 100.0.

Fig 6. Results obtained with the same model as Fig 4, except that x_q1(0) = 100.0 and ν_q1 = 0.01.

Fig 7. Test simulations of the population dynamics of three imatinib-resistant differentiated cell clones and of the total number of differentiated cells based on model C (Eq (8)) for parameters x_q1(0) = 100.0, ν_q1 = 0.01, θ_q1 = 1.5 × 10⁷ and ν_c1 = 0.1.

The panels (a), (b) and (c) correspond to the threshold settings θ_s2 = 10.0, 100.0 and 500.0, respectively. The other parameters employed for the simulations are compiled in Table 2. Color scheme: x_d1 (blue), x_d2 (red), x_d3 (green) and y (black). The ordinate unit is number of cells / ml blood.

Fig 8. Results obtained with the same model as Fig 7, except that ν_c1 = 0.50.

Fig 9. Results obtained with the same model as Fig 7, except that ν_c1 = 1.00.

Fig 10. Fit to PP14 using model C, mutations of stem cells are not taken into account (ν₂ = 0.0, ν₃ = 0.0).

The experimental values for clones Y253H (blue circles), F317L (red squares) and V299L_2 (green diamonds) are considered, clone V299L_1 is ignored by the fit. The evolution of stem and differentiated cell populations is shown in panels (a) and (b), respectively. The teal curve in panel (a) corresponds to the quiescent population of stem cell clone Y253H. In panel (b), the following identifications are made: x_d1(t)(blue curve)↔Y253H, x_d2(t)(red curve)↔F317L, x_d3(t)(green curve)↔V299L_2. The black curve and triangles correspond to the fitted and experimental values of the total leukemic burden, respectively. The ordinate unit of panel (b) refers to the differentiated cell BCR-ABL1 / GUS ratios of the respective clones. While panel (b) reproduces also clinical datasets, the ordinate of panel (a) specifies the size of the stem cell populations in arbitrary units, the scale is determined by the parameters a_i. The parameter set employed for this simulation is compiled in Table 3.

Fig 11. Description is the same as for Fig 10, except that mutations x_s1(t) → x_s3(t) are included in the simulation (ν₃≠0, cf. Table 3).

Fig 12. Fit to PP15 using model C, including the experimental values for clones Y253H (blue circles) and T315I (red squares).

Mutations of stem cells are not taken into account (ν₂ = 0.0, ν₃ = 0.0). The evolution of stem and differentiated cell populations is shown in panels (a) and (b), respectively. The teal curve in panel (a) corresponds to the quiescent population of stem cell clone Y253H. In panel (b), the following identifications are made: x_d1(t)(blue curve)↔Y253H, x_d2(t)(red curve)↔T315I, x_d3(t)(green curve)↔X. The black curve and triangles correspond to the fitted and experimental values of the total leukemic burden, respectively. The ordinate unit of panel (b) refers to the differentiated cell BCR-ABL1 / GUS ratios of the respective clones. While panel (b) reproduces also clinical datasets, the ordinate of panel (a) specifies the size of the stem cell populations in arbitrary units, the scale is determined by the parameters a_i. The parameter set employed for this simulation is compiled in Table 3. This simulation investigates the role of a hypothetical third clone X that is not explicitly identified by experiment. The dashed-dotted green line represents stem and differentiated cell populations of this hypothetical third clone.

Fig 13. Description is the same as for Fig 12, except that mutations x_s1(t) → x_s3(t) are included in the simulation (ν₃≠0, cf. Table 3).

Fig 14. Fit to PP15 using model C (with populations x_s3(t) and x_d3(t) set to 0.0), including the experimental values for clones Y253H (blue circles) and T315I (red squares).

Mutations of stem cells are not taken into account (ν₂ = 0.0, ν₃ = 0.0). The evolution of stem and differentiated cell populations is shown in panels (a) and (b), respectively. The teal curve in panel (a) corresponds to the quiescent population of stem cell clone Y253H. In panel (b), the following identifications are made: x_d1(t)(blue curve)↔Y253H, x_d2(t)(red curve)↔T315I. The black curve and triangles correspond to the fitted and experimental values of the total leukemic burden, respectively. The ordinate unit of panel (b) refers to the differentiated cell BCR-ABL1 / GUS ratios of the respective clones. While panel (b) reproduces also clinical datasets, the ordinate of panel (a) specifies the size of the stem cell populations in arbitrary units, the scale is determined by the parameters a_i. The parameter set employed for this simulation is compiled in Table 3.