Treatment with integrase inhibitor suggests a new interpretation of HIV RNA decay curves that reveals a subset of cells with slow integration

Abstract

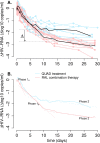
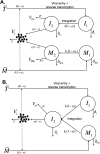
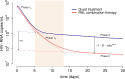
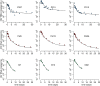
The kinetics of HIV-1 decay under treatment depends on the class of antiretrovirals used. Mathematical models are useful to interpret the different profiles, providing quantitative information about the kinetics of virus replication and the cell populations contributing to viral decay. We modeled proviral integration in short- and long-lived infected cells to compare viral kinetics under treatment with and without the integrase inhibitor raltegravir (RAL). We fitted the model to data obtained from participants treated with RAL-containing regimes or with a four-drug regimen of protease and reverse transcriptase inhibitors. Our model explains the existence and quantifies the three phases of HIV-1 RNA decay in RAL-based regimens vs. the two phases observed in therapies without RAL. Our findings indicate that HIV-1 infection is mostly sustained by short-lived infected cells with fast integration and a short viral production period, and by long-lived infected cells with slow integration but an equally short viral production period. We propose that these cells represent activated and resting infected CD4+ T-cells, respectively, and estimate that infection of resting cells represent ~4% of productive reverse transcription events in chronic infection. RAL reveals the kinetics of proviral integration, showing that in short-lived cells the pre-integration population has a half-life of ~7 hours, whereas in long-lived cells this half-life is ~6 weeks. We also show that the efficacy of RAL can be estimated by the difference in viral load at the start of the second phase in protocols with and without RAL. Overall, we provide a mechanistic model of viral infection that parsimoniously explains the kinetics of viral load decline under multiple classes of antiretrovirals.

Fig 1. Viral dynamics after the initiation of treatment with or without RAL.

(A) Blue and pink lines show the viral load relative to baseline for study participants in the QUAD treatment and RAL-combination therapy, respectively. Black lines represent the median values for each group. In the last phase, between about day 15 and day 30, the viral load in the RAL-combination participants is ~1-log lower (Δ~90% reduction) than the viral load in the quad-therapy group participants. (B) The median viral load profiles for each group present two phases of decay (1a and 2), but in addition the RAL-combination therapy includes an intermediate phase, 1b.

Fig 2. Schematics of the models.

(A) The standard model with pre- and post-integration phases of infection. We follow two types of target cells that after infection will be short-lived, $\overline{T}$, or long-lived, $\overline{M}$. Target cells, $\overline{T}$, are infected by infectious virus, V_i, at rate $\beta \overline{T}{V}_i$. The infection can be blocked by the activity of RTIs with effectiveness η. These infected cells, I₁, are lost at rate δ₁, or can undergo provirus integration at rate k and become productively infected cells I₂. InSTIs block integration with efficacy ω. Cells with integrated provirus, I₂, are lost at rate δ₂. Virions are produced by these cells at rate p per cell and are cleared from the circulation at rate c per virion. Protease inhibitors block the production of infectious virus V_Ii, and lead to production of non-infectious virus V_Ini, with efficacy ε. The subscripts I and M are used to distinguish virions produced by short-lived and long-lived infected cells, respectively. The dynamics of long-lived cells are similar, but possibly with different rates as indicated. (B) The slow and rapid integration (SRI) model. The SRI model proposes that both short-lived cells with fast integration (I₁) and long-lived cells with slow integration (M₁) generate productively infected cells that die quickly (I₂) (i.e. δ₂ = δ_M2).

Fig 3. Predicted viral load decay for the quad and RAL-combination treatments using the best fit of the SRI model (Eq (1) when δ₂ = δ_M2) to the data.

The estimated population parameters for each treatment group where used to plot the viral load decline under the effect of RAL+RTI (red) and quad therapy (blue). The dotted blue and red lines show the analytical approximation for the second phase of decay for quad therapy and RAL-combination therapy, respectively (see equation S.14 in S1 Text). The shadowed section highlights phase 1b for RAL-combination therapy. The viral load at the start of phase 2 in patients under RAL-based therapy is reduced with respect to the corresponding level in RAL-free therapy by a factor of $1-(1-\omega )e^{k_1\omega t}$. We fixed the values of the following parameters (see text for details): V_I(0)/V(0) = 0.98, δ_M1 = 0.02 day^-1, k = 2.6 day^-1 and c = 23 day^-1 based on previous studies [14,16,39]. In addition, for RAL combination we used η = 0.95, ε = 0 and ω = 0.94, and for the quad therapy η = ε = 0.95 and ω = 0 [14]. The estimated best-fit population parameters are (estimated standard deviation in parenthesis): δ₁ = 0.23 (0.04) day^-1, k₁ = 0.017 (0.01) day^-1, δ₂ = 0.85 (0.07) day^-1 and V(0) = 4.8 (0.07).

Fig 4. Representative individual fits for the three datasets.

Blue, red and green circles represent HIV RNA measurements for the quad-based-, RAL-combination- and RAL-mono therapy, respectively. Solid black lines represent best fits from the SRI model using the mixed-effects approach. Parameter estimates for each individual are presented in Table E in S1 Text.