Reconstructing anatomy from electro-physiological data

Abstract

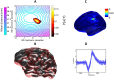
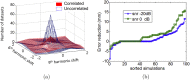
Here we show how it is possible to make estimates of brain structure based on MEG data. We do this by reconstructing functional estimates onto distorted cortical manifolds parameterised in terms of their spherical harmonics. We demonstrate that both empirical and simulated MEG data give rise to consistent and plausible anatomical estimates. Importantly, the estimation of structure from MEG data can be quantified in terms of millimetres from the true brain structure. We show, for simulated data, that the functional assumptions which are closer to the functional ground-truth give rise to anatomical estimates that are closer to the true anatomy.

Keywords: Brain anatomy; Fourier spherical harmonics; MEG/EEG brain imaging; Negative variational free energy.

Fig. 1

(a) Shows a one-many mapping for different task data. For any task (or period of time) i the same MEG data (B) can be described by more than one current distribution (J). The current distribution that is estimated depends on prior functional assumptions (1 or 2, which could correspond to minimum norm and beamformer for example). At a different time (or task) $i+1$, new MEG data can be explained by another quite distinct set of possible current distributions. (b) Shows the many-one mapping one should expect from estimating anatomy. In this case although there will be many different possible anatomical structures which could underlie any one set of measurements $B_i$, this set of structures must be close to the set explaining the data at time $B_{i+1}$. Indeed, as more MEG data is recorded, the space of anatomy that could explain all of the data gets smaller and smaller. As the anatomy is contingent on reasonable functional priors, only the correct functional assumptions (and forward models) will lead us to the true anatomy.

Fig. 2

A) Two dimensional space of candidate brains corresponding to distortions in the 6th and 9th spherical harmonics by two standard deviations of normal variation. The surface at the origin (central image) is the average brain (over subjects in anatomical database), and caricature brains develop for increasing distortions. B) Schematic of the MEG sensors measuring magnetic field change around the subject's head. C) Average change (over trials, from 274 sensors) in magnetic field due to current flow in the subject's cortex (taken to be an unknown structure) time-locked to a finger movement.

Fig. 3

Contour plots around the edges of the figure show the Free energy obtained by solving the MEG inverse problem with eight different datasets over a grid of 81 distorted candidate brains. All datasets (except the top right panel) give rise to a similar global maximum close to the origin (or average brain shape) showing the stability of the approach to initial conditions. The centre panel shows the independently computed mean RMS error (in mm) between the space of deformed brains and the true brain structure (which is being estimated in the surrounding panels).

Fig. 4

A) Hot colours (red/white) show the 95% posterior probability estimate of cortical structure based on the MEG data; cool colours (blue/purple) show the average Euclidean distance from points in the true brain structure to corresponding points in each brain in the library. Panel B) shows the most likely anatomical model given the MEG data (the cortical structure at the peak of the probability distribution in panel A); the red contour shows the 95% confidence interval for this structural estimate. C) Shows estimated electrical activity on the inflated cortical surface (from panel B) at $t=72$ ms post button press. D) Shows the time-course of this activity (extracted from MNI location -46, -16, 50 mm); the shaded region shows the 95% confidence intervals on this estimate.

Fig. 5

Control conditions. (a) Estimate of structure (point of maximal Free energy) using very low SNR data (the data from Fig. 3, run 1, filtered between 100 and 200 Hz). In this case the plausible brain structures –close to (0,0)– are the least probable. (b) Shows the two different contour plot dimensions in 1D for the sensitivity to anatomy using either the Nolte single shell model (as above), or a single sphere model. Note that both forward models peak at the same approximate anatomical location (but that the Nolte model is much more likely).

Fig. 6

Anatomical reconstructions of 200 datasets (100 correlated and 100 uncorrelated source pairs) simulated on the cortical surface at the origin of the space of brains (in Fig. 2). (a) Shows the histogram of the most likely anatomy when data were reconstructed using beamformer (uncorrelated) priors for correlated (red) and uncorrelated (open mesh) source pairs at 0 dB SNR. (b) Shows the (sorted) reduction in anatomical reconstruction error (in mm) when the anatomy was reconstructed based on uncorrelated rather than correlated source pairs (at same location and SNR) for -20 (blue squares) and 0 dB (green circles) SNR. For example, at 0 dB SNR anatomical reconstruction accuracy improved in all but 15% of cases when the source pairs were uncorrelated (congruent with the functional prior). This contrast (between appropriate and inappropriate priors) in anatomical reconstruction accuracy was less marked at lower SNR.