John's Equation-based Consistency Condition and Corrupted Projection Restoration in Circular Trajectory Cone Beam CT

Abstract

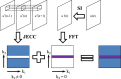
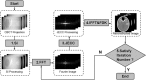
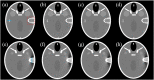
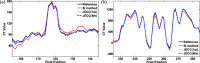
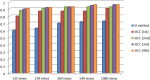
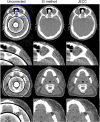
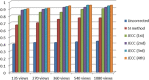
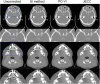
In transmitted X-ray tomography imaging, the acquired projections may be corrupted for various reasons, such as defective detector cells and beam-stop array scatter correction problems. In this study, we derive a consistency condition for cone-beam projections and propose a method to restore lost data in corrupted projections. In particular, the relationship of the geometry parameters in circular trajectory cone-beam computed tomography (CBCT) is utilized to convert an ultra-hyperbolic partial differential equation (PDE) into a second-order PDE. The second-order PDE is then transformed into a first-order ordinary differential equation in the frequency domain. The left side of the equation for the newly derived consistency condition is the projection derivative of the current and adjacent views, whereas the right side is the projection derivative of the geometry parameters. A projection restoration method is established based on the newly derived equation to restore corrupted data in projections in circular trajectory CBCT. The proposed method is tested in beam-stop array scatter correction, metal artifact reduction, and abnormal pixel correction cases to evaluate the performance of the consistency condition and corrupted projection restoration method. Qualitative and quantitative results demonstrate that the present method has considerable potential in restoring lost data in corrupted projections.

Figure 1

Geometry configuration of circular trajectory CBCT.

Figure 2

Illustration of the corrupted projection restoration capabilities of JECC and SI in the frequency domain.

Figure 3

Workflow of the JECC method in circular trajectory CBCT.

Figure 4

Configuration of moving BSA scatter correction case. (a) BSA in odd-numbered views (mode I); (b) BSA in even-numbered views (mode II); (c) projections in a circular trajectory by moving the BSA scatter correction protocol. The odd-numbered views use mode I in (a), and the even-numbered views use mode II in (b).

Figure 5

In-house bench-top CBCT system for raw projection acquisition.

Figure 6

JECC performance on different slices. (a) Reference image on the 100th slice; (b–d) images on the 100th slice reconstructed using the SI method, JECC 1st iteration, and JECC 4th iteration, respectively; (e) reference image on the 80th slice; (f–h) images on the 80th slice reconstructed using the SI method, JECC 1st iteration, and JECC 4th iteration, respectively.

Figure 7

Image profiles of the results in Fig. 6. (a) Profiles across the 95th to 145th columns in the 255th row of the results indicated by the blue line in Fig. 6(a); (b) profiles across the 225th to 285th rows in the 401th column of the results indicated by the blue line in Fig. 6(e).

Figure 8

Comparison of the different methods in terms of UQI.

Figure 9

Image without correction and images reconstructed using the SI method and the JECC method. The first row presents the images on the 190th slice, and the third row presents the images on the 220th. The second and fourth rows present the magnified ROIs marked with yellow squares in the images in the first and third rows.

Figure 10

Images corrected with SI method and the proposed method. The first and third rows present two representative slices. The second and fourth rows present the zoomed ROIs marked with blue dashed squares in the first and third rows.

Figure 11

Image profiles of the results in Fig. 9. (a) Profiles across the 315th to 375th rows in the 145th column of the results indicated by a blue line in the top row in Fig. 9; (b) profiles across the 345th to 385th rows in the 170th column of the results indicated by a blue line in the third row in Fig. 9.

Figure 12

Comparison of the different methods in terms of UQI.

Figure 13

Bilateral hip prostheses simulation. The transverse, sagittal, and coronal views are displayed in the first, second, and third rows, respectively.

Figure 14

Image Profiles of the results in Fig. 13. (a) Profiles indicated by the blue dashed line in transverse view; (b) profiles indicated by the blue dashed line in coronal view.

Figure 15

Two clinical cases are displayed here. The first row is the head case with a brain stimulator and the second row presents the corresponding magnified ROIs which are the blue dashed squares containing the metal implant, the bottom two rows present the dental case with three dental fillings on the back teeth and one dental filling on the front tooth.

Figure 16

Frequency domain illustrations of the same image. (a) Frequency domain of the image obtained using the SI method; (b) frequency domain of the image obtained using the JECC method; (c) frequency domain of the difference between the images in (a) and (b).