Cellular mechanosensing of the biophysical microenvironment: A review of mathematical models of biophysical regulation of cell responses

Abstract

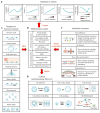
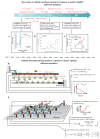
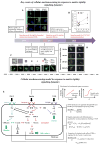
Cells in vivo reside within complex microenvironments composed of both biochemical and biophysical cues. The dynamic feedback between cells and their microenvironments hinges upon biophysical cues that regulate critical cellular behaviors. Understanding this regulation from sensing to reaction to feedback is therefore critical, and a large effort is afoot to identify and mathematically model the fundamental mechanobiological mechanisms underlying this regulation. This review provides a critical perspective on recent progress in mathematical models for the responses of cells to the biophysical cues in their microenvironments, including dynamic strain, osmotic shock, fluid shear stress, mechanical force, matrix rigidity, porosity, and matrix shape. The review highlights key successes and failings of existing models, and discusses future opportunities and challenges in the field.

Keywords: Biomechanics; Cellular mechanosensing; Focal adhesions; Mathematical modeling; Mechanobiology; Signaling pathway.

Figure 1. Application of cellular mechanosensing models in mechanobiology

Cells sense and respond biophysical cues such as dynamic strain, osmotic shock, shear flow, external forces, matrix rigidity, and steric constraints. For example, cells have bigger focal adhesions on stiffer substrata; cells can actively regulate their volume in response to osmotic shock; and cells reorient in response to mechanical strain. This review summarizes mathematical models based upon different cellular mechanosensing components that have been applied to interpret these phenomena.

Figure 2. Cellular mechanosensing in response to dynamic strain

(A) Under conditions simulating mammalian long bone growth (e.g., a static or quasi-static stretch), cultured myocytes respond to mechanical forces by lengthening and orienting along the direction of stretch [82]. (B) Many tissue cells (e.g., fibroblasts and endothelial cells) prefer to align perpendicular to the direction of applied cyclic strain, especially at high frequency and larger stretching magnitude [83]. (C) Cells can reorient to a uniform angle in response to cyclic stretching of the underlying substrate [84]. (D) A mechanical model of SFs, showing adhesion complexes, myosin motors and actin filaments. Myosin motors generate force between antiparallel actin filament bundles, one of which is anchored to the matrix by adhesion complexes. Proteins in adhesion and actin filaments system are drawn as masses on springs in order to indicate how they function in the model.

Figure 3. Cellular mechanosensing in response to osmotic shock, fluid shear stress and mechanical forces

(A) The 3D random network model of the actin cytoskeleton to study the nuclear deformation under micropipette aspiration [124]. (B) The multi-structural 3D finite element (FE) model can be used to study how cytoskeletal mechanical properties affect cell responses under AFM indentation [121]. (C) A 2D cable network model predicts how stress is transmitted through the actin cytoskeletons of adherent cells and consequentially distributed at focal adhesions sites (FAs) [120]. (D) Myosin and α-actinin accumulation increase at the pipette tip and filamin increases in the neck region during micropipette aspiration [117]. (E) Steady state cellular volume increases with increasing extracellular osmotic pressure [71]. (F) Schematic of the model prediction of volumetric changes in response to osmotic shock. The model includes the Rho signaling pathway, which activates myosin assembly and active contraction in the cell cortex. At mechanical equilibrium, the membrane tension balances both osmotic pressure and active cortical contraction.

Figure 4. Cellular mechanosensing in response to matrix rigidity: adhesion dynamics

(A) Neurons have higher actin flow rate on stiffer substrata [147]. (B–C) The distinct actin flow/matrix rigidity relationships in breast myoepithelial cells and fibroblasts [10, 25]. (D) Schematic of the uniaxial molecular clutch model. Actin polymerization and depolymerization at the tips of filopodia are coupled to the substrate through molecular clutches, and these molecular clutches resist the retrograde actin flow driven by myosin motors and membrane fluctuations. With increasing tension, the following transformations of molecular clutches are possible: talin unfolding and refolding, clutch reinforcement by vinculin binding, signal activation from clutch reconfiguration, and weakest-link rupture. (E) Schematic of the 2D molecular-mechanical adhesion model. Each molecule may bind to the substrate through a flexible spring, and may transition from a circular to an elliptical state under mechanical loading.

Figure 5. Cellular mechanosensing in response to matrix rigidity: signaling dynamics

(A) The lineage of mesenchymal stem cells (MSCs) is strongly affected by the modulus of the substratum upon which they are cultured [26]. (B) The conversion of fibroblasts into myofibroblast is also regulated by external mechanical cues [73]. (C) YAP/TAZ nuclear translocation has been shown to be influenced by ECM stiffness and shape [145]. (D) FDGF can significantly increase the lifetime and size of CDRs on stiff substrata [14]. (E) Signaling pathway dynamic model for cell shape, migration and differentiation. The matrix rigidity is transduced into intracellular signals via adhesion molecules such as FAK and Src. Adhesion-mediated mechanosensing signals include Rho/ROCK/myosin II, Rho/mDia1/F-actin, SF/YAP/TEAD and SF/MAL/SRF. Other related signals related to soluble factors are TGFβ/p38/αSMA and PDGF/Rac/Arp2/3. A synergistic effect between the mechanical sensing and the chemical signals is predicted due in part to the interaction of Rac/Rho and ERK/p38.

Figure 6. Cellular mechanosensing in response to matrix rigidity: nucleus lamin-A dynamics

(A) Lamin-A concentration increases with increasing matrix stiffness [11]. (B) The levels of collagen-1 and cardiac myosin increase first and then reach a maximum value during the development of embryonic chick hearts [170]. (C) Lamin-A is found more in the basal than the apical nuclear envelope of fibroblasts adhering to stiff (but not soft) polyacrylamide hydrogels [206]. (D) Schematic of the gene circuit model predicting how matrix rigidity regulates levels of nuclear lamin-A. Stiffer matrices enhance cellular contraction and increase the tension in nuclear lamin layer, thereby decreasing the lamin-A degradation rate. Tension acting on the nucleus by stress fibers can also influence transcription factors associated with nucleoplasm shuttling, which can further regulate lamin-A expression.

Figure 7. Cellular mechanosensing of steric constraints

(A) A biphasic relationship exists between cell migration rate and fibronectin density: cell migration rate is maximal at a particular fibronectin density) [174]. (B) A biphasic relationship exists between cell migration rate the cross-sectional are of a microfluidic channel [175]. (C) Tractions are elevated at the corners of cell spread on micropatterned geometries [176]. (D) A 3D integrated dynamic model of cell migration on a curved substrate. The plasma and nuclear membranes are modeled as elastic meshes that interact with the ECM through integrin-fibronectin bonds, and with each other through actin stress fibers. (E) A cellular Potts model, in which cells which are modeled as a collection of spins, and overall energy during cell spreading is evaluated as cells probe possible expansion onto nodes of a regular lattice.