Synapse fits neuron: joint reduction by model inversion
- PMID: 28689352
- PMCID: PMC5506247
- DOI: 10.1007/s00422-017-0722-1
Synapse fits neuron: joint reduction by model inversion
Abstract
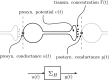
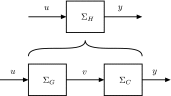
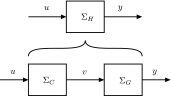
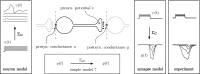
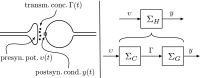
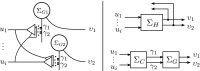
In this paper, we introduce a novel simplification method for dealing with physical systems that can be thought to consist of two subsystems connected in series, such as a neuron and a synapse. The aim of our method is to help find a simple, yet convincing model of the full cascade-connected system, assuming that a satisfactory model of one of the subsystems, e.g., the neuron, is already given. Our method allows us to validate a candidate model of the full cascade against data at a finer scale. In our main example, we apply our method to part of the squid's giant fiber system. We first postulate a simple, hypothetical model of cell-to-cell signaling based on the squid's escape response. Then, given a FitzHugh-type neuron model, we derive the verifiable model of the squid giant synapse that this hypothesis implies. We show that the derived synapse model accurately reproduces synaptic recordings, hence lending support to the postulated, simple model of cell-to-cell signaling, which thus, in turn, can be used as a basic building block for network models.
Keywords: Conductance-based models; Inverse systems; State-space realizations; Synaptic transmission.
Figures





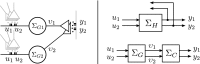
Similar articles
-
Afferent synaptic drive of rat medial nucleus tractus solitarius neurons: dynamic simulation of graded vesicular mobilization, release, and non-NMDA receptor kinetics.J Neurophysiol. 1995 Oct;74(4):1529-48. doi: 10.1152/jn.1995.74.4.1529. J Neurophysiol. 1995. PMID: 8989391
-
Transmission in the squid giant synapse: a model based on voltage clamp studies.J Physiol (Paris). 1980 Sep;76(5):413-8. J Physiol (Paris). 1980. PMID: 6256531
-
A cholinergic model synapse to elucidate protein function at presynaptic terminals.Neurosci Res. 2007 Apr;57(4):491-8. doi: 10.1016/j.neures.2006.12.015. Epub 2007 Jan 10. Neurosci Res. 2007. PMID: 17287041
-
A review of the integrate-and-fire neuron model: II. Inhomogeneous synaptic input and network properties.Biol Cybern. 2006 Aug;95(2):97-112. doi: 10.1007/s00422-006-0082-8. Epub 2006 Jul 5. Biol Cybern. 2006. PMID: 16821035 Review.
-
A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input.Biol Cybern. 2006 Jul;95(1):1-19. doi: 10.1007/s00422-006-0068-6. Epub 2006 Apr 19. Biol Cybern. 2006. PMID: 16622699 Review.
References
-
- Clay JR. Excitability of the squid giant axon revisited. J Neurophysiol. 1998;80:903–913. - PubMed
-
- Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. Cambridge: The MIT Press; 2001.
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

