Spin diffusion from an inhomogeneous quench in an integrable system
- PMID: 28703138
- PMCID: PMC5554798
- DOI: 10.1038/ncomms16117
Spin diffusion from an inhomogeneous quench in an integrable system
Abstract
Generalized hydrodynamics predicts universal ballistic transport in integrable lattice systems when prepared in generic inhomogeneous initial states. However, the ballistic contribution to transport can vanish in systems with additional discrete symmetries. Here we perform large scale numerical simulations of spin dynamics in the anisotropic Heisenberg XXZ spin 1/2 chain starting from an inhomogeneous mixed initial state which is symmetric with respect to a combination of spin reversal and spatial reflection. In the isotropic and easy-axis regimes we find non-ballistic spin transport which we analyse in detail in terms of scaling exponents of the transported magnetization and scaling profiles of the spin density. While in the easy-axis regime we find accurate evidence of normal diffusion, the spin transport in the isotropic case is clearly super-diffusive, with the scaling exponent very close to 2/3, but with universal scaling dynamics which obeys the diffusion equation in nonlinearly scaled time.
Conflict of interest statement
The authors declare no competing financial interests.
Figures
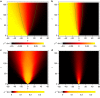
 (a,b) and current (c,d) profile j(x, t)=tr(ρ(t)jx) for the isotropic point Δ=1 (a,c), and Δ=2 (b,d), following an inhomogeneous quench. One can see that the spreading is much faster for Δ=1, in both cases though it is slower than ballistic. Dashed green curves guide the eye towards scaling x∼t2/3 in a, and x∼t1/2 in (b). Data are shown for n=320 and small initial polarization μ=π/1,800.
(a,b) and current (c,d) profile j(x, t)=tr(ρ(t)jx) for the isotropic point Δ=1 (a,c), and Δ=2 (b,d), following an inhomogeneous quench. One can see that the spreading is much faster for Δ=1, in both cases though it is slower than ballistic. Dashed green curves guide the eye towards scaling x∼t2/3 in a, and x∼t1/2 in (b). Data are shown for n=320 and small initial polarization μ=π/1,800.


References
-
- Takahashi M. Thermodynamics of One-Dimensional Solvable Models Cambridge University Press (1999).
-
- Polkovnikov A., Sengupta K., Silva A. & Vengalattore M. Colloquium: nonequilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 83, 863–883 (2011).
-
- Bloch I., Dalibard J. & Nascimbene S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267–276 (2012).
-
- Choi J.-Y. et al.. Exploring the many-body localization transition in two dimensions. Science 352, 1547–1552 (2016). - PubMed
-
- Calabrese P., Essler F. H. L. & Mussardo G. Special issue on ‘Quantum Integrability in Out of Equilibrium Systems’. J. Stat. Mech. 2016, 064001 (2016).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

