A Predictive Mathematical Modeling Approach for the Study of Doxorubicin Treatment in Triple Negative Breast Cancer

Abstract

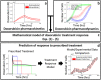
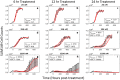
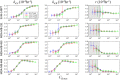
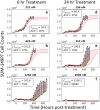
Doxorubicin forms the basis of chemotherapy regimens for several malignancies, including triple negative breast cancer (TNBC). Here, we present a coupled experimental/modeling approach to establish an in vitro pharmacokinetic/pharmacodynamic model to describe how the concentration and duration of doxorubicin therapy shape subsequent cell population dynamics. This work features a series of longitudinal fluorescence microscopy experiments that characterize (1) doxorubicin uptake dynamics in a panel of TNBC cell lines, and (2) cell population response to doxorubicin over 30 days. We propose a treatment response model, fully parameterized with experimental imaging data, to describe doxorubicin uptake and predict subsequent population dynamics. We found that a three compartment model can describe doxorubicin pharmacokinetics, and pharmacokinetic parameters vary significantly among the cell lines investigated. The proposed model effectively captures population dynamics and translates well to a predictive framework. In a representative cell line (SUM-149PT) treated for 12 hours with doxorubicin, the mean percent errors of the best-fit and predicted models were 14% (±10%) and 16% (±12%), which are notable considering these statistics represent errors over 30 days following treatment. More generally, this work provides both a template for studies quantitatively investigating treatment response and a scalable approach toward predictions of tumor response in vivo.

Figure 1

Overview of cell-line specific modeling framework for doxorubicin treatment response prediction. A series of time-resolved fluorescence microscopy experiments were performed to quantify both the uptake of doxorubicin into TNBC cell lines (a) as well as the response of those cell lines to various doxorubicin treatments (b). Data from these experiments were used to fit the model (i.e., Eqs (1–5)) of treatment response in TNBC (c). After training the model on observed data, the model can be initialized with a cell count and a prescribed treatment timecourse to predict cell population dynamics following the proposed treatment (d). These predictions can then be compared to experimental results.

Figure 2

Overview of Doxorubicin Compartment Modeling. Doxorubicin pharmacokinetics is described with a three compartment model, illustrated in (a) and described by Eqs (1–3). To parameterize this model, each cell line is serially imaged via brightfield (b) and fluorescent microscopy (c) to monitor doxorubicin concentration over time. Images are separated into extracellular and intracellular (red overlay) compartments. As fluorescence intensity is proportional to doxorubicin concentration (d), the image intensities are converted into concentration, and extracellular and intracellular concentration timecourses are extracted from these images (e). Finally, the model is fit to these timecourses (e), and the model fit with 95% confidence interval are overlaid on the data. Experimentally-derived model parameter values with 95% CIs are reported for each TNBC cell line investigated (f–h).

Figure 3

Impact of doxorubicin concentration and exposure time on response of SUM-149PT cells. The SUM-149PT cell line was plated and serially imaged via fluorescence microscopy for 30 days following time-resolved doxorubicin treatments. Nuclear counts from these images are displayed below in black with error bars representing the 95% CI from the six experimental replicates. These counts are fit to Eqs (4 and 5) as described Section 2.5. Model fits with 95% CI are superimposed on the cell counts. The SUM-149PT cell line demonstrated a graded dose-dependent and time-dependent response to doxorubicin treatment. At low concentrations, no appreciable treatment effect is noted regardless of exposure time (a–c). At higher concentrations and exposure times, the population growth rate slows (d,e), eventually demonstrating a prolonged response to therapy with subsequent regrowth of the population (f–h). At very high concentrations and exposure times, no population regrowth is observed (i).

Figure 4

Dose-response curves in a panel of TNBC cell lines. Each cell line was plated and serially imaged via fluorescence microscopy for 30 days following a 6-hour doxorubicin treatment. Nuclear counts from these images are displayed below in black with error bars representing the 95% CI from the six experimental replicates. Each column corresponds to an individual cell line, and each row corresponds to a doxorubicin concentration. These counts are fit to Eqs (4–5) as described Section 2.5. Model fits with 95% CI are superimposed on the cell counts. While there is significant variability in cell line sensitivity to doxorubicin treatment, the dynamics of each cell line follows a similar pattern: following treatment the population growth rate slows as a function of treatment, and depending on the treatment duration and concentration, a rebound in population growth rate is observed.

Figure 5

Parameter fits from Eq. (5) in a panel of TNBC cell lines as a function of C _B,max. The parameters in Eq. (5) are fit to each treatment condition as described in Section 2.5 and plotted with 95% confidence intervals against the cell-line specific simulated C _B,max from Eqs (1–3). The blue X’s, red O’s, and green Δ’s represent the parameter fits extracted from the 6, 12, and 24 hour exposure time datasets respectively. Model parameters estimated from each exposure time appear to collapse on each other, when described by C _B,max – a summary statistic of each treatment condition. This indicates that the compartment model is effective at describing the treatments. Further, given that each cell line appears to follow a single trajectory for each parameter, this model can be used to predict cell population response to any predefined input function. The gray areas for parameter r represent treatment ranges where the total-order sensitivity index (S _TI), which describes the effect of parameter variation on model prediction variation, is ≤0.3. Thus the large variance in parameter estimates here has a limited impact on model predictions.

Figure 6

Model prediction results in SUM-149PT cell line. As described in Section 2.6, model parameters (k _d,A, θ in Eq. (5A) and k _d,B, r, θ in Eq. (5B)) were fit to each treatment condition in the training set (12-hour exposure dataset). These parameter fits were then described by local regression models to generate model parameter estimates for treatments in the test set (6- and 24-hour exposure datasets). Final predictions represent a weighted average of Eq. (5A) and (B), and a bootstrap analysis was used to generate a 95% confidence interval for these predictions (red overlay). A series of predictions in the SUM-149PT cell line following 6- and 24-hour doxorubicin treatments at three doxorubicin concentrations are shown. Nuclear counts from these experiments are displayed in black with error bars representing the 95% CI from the six experimental replicates. Each column corresponds to an exposure time. The response of a TNBC cell line can be predicted using experimentally-derived PK and PD parameters.