A random effects meta-analysis model with Box-Cox transformation

Abstract

Background: In a random effects meta-analysis model, true treatment effects for each study are routinely assumed to follow a normal distribution. However, normality is a restrictive assumption and the misspecification of the random effects distribution may result in a misleading estimate of overall mean for the treatment effect, an inappropriate quantification of heterogeneity across studies and a wrongly symmetric prediction interval.

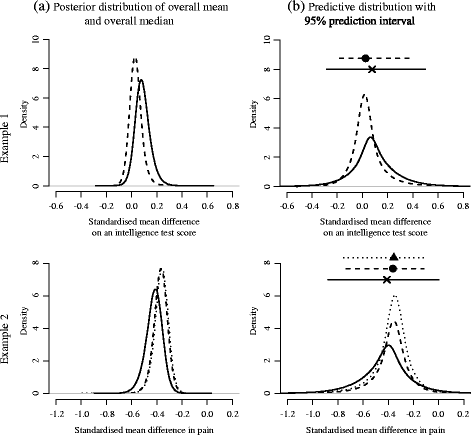
Methods: We focus on problems caused by an inappropriate normality assumption of the random effects distribution, and propose a novel random effects meta-analysis model where a Box-Cox transformation is applied to the observed treatment effect estimates. The proposed model aims to normalise an overall distribution of observed treatment effect estimates, which is sum of the within-study sampling distributions and the random effects distribution. When sampling distributions are approximately normal, non-normality in the overall distribution will be mainly due to the random effects distribution, especially when the between-study variation is large relative to the within-study variation. The Box-Cox transformation addresses this flexibly according to the observed departure from normality. We use a Bayesian approach for estimating parameters in the proposed model, and suggest summarising the meta-analysis results by an overall median, an interquartile range and a prediction interval. The model can be applied for any kind of variables once the treatment effect estimate is defined from the variable.

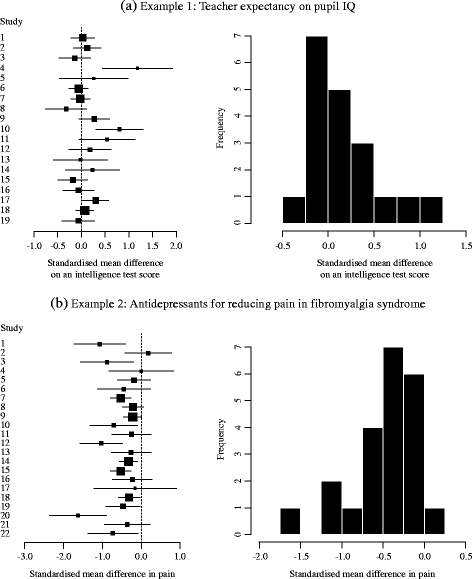
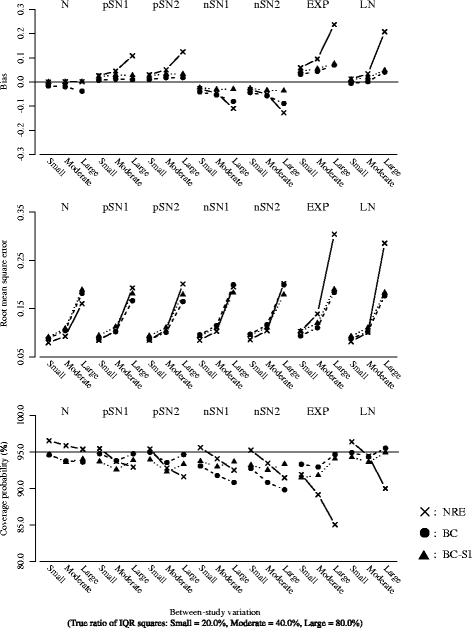
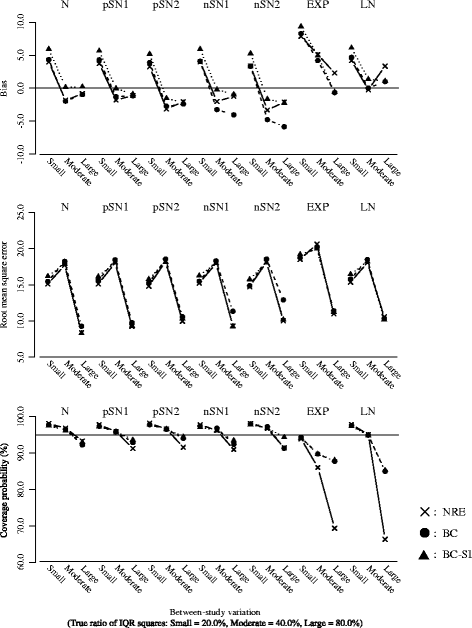
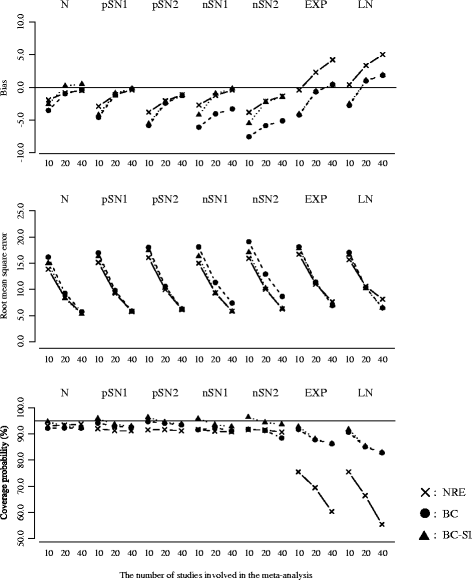
Results: A simulation study suggested that when the overall distribution of treatment effect estimates are skewed, the overall mean and conventional I ² from the normal random effects model could be inappropriate summaries, and the proposed model helped reduce this issue. We illustrated the proposed model using two examples, which revealed some important differences on summary results, heterogeneity measures and prediction intervals from the normal random effects model.

Conclusions: The random effects meta-analysis with the Box-Cox transformation may be an important tool for examining robustness of traditional meta-analysis results against skewness on the observed treatment effect estimates. Further critical evaluation of the method is needed.

Keywords: Box-Cox transformation; Meta-analysis; Random effects model; Skewed data.

Fig. 1

Forest plot and histogram. a 19 experiments investigating teacher expectancy on pupil IQ, b 22 studies investigating antidepressants for reducing pain in fibromyalgia syndrome

Fig. 2

Bias, RMSE and coverage probability of the overall mean or the overall median for the scenario of the number of studies k=20. The overall mean from the normal random effects model (cross/solid line), and those of the overall median from the proposed model (black circle/broken line: Box-Cox transformation, black triangle/dotted line: Box-Cox transformation with the sign inversion)

Fig. 3

Bias, RMSE and coverage probability of the I ² or the ratio of IQR squares for the scenario of the number of studies k=20. The I ² from the normal random effects model (cross/solid line), and those of the ratio of IQR squares from the proposed model (black circle/broken line: Box-Cox transformation, black triangle/dotted line: Box-Cox transformation with the sign inversion)

Fig. 4

Bias, RMSE and coverage probability of the overall mean or the overall median for the scenario of true ratio of IQR squares = 80.0% (large between-study variation). The overall mean from the normal random effects model (cross/solid line), and those of the overall median from the proposed model (black circle/broken line: Box-Cox transformation, black triangle/dotted line: Box-Cox transformation with the sign inversion)

Fig. 5

Bias, RMSE and coverage probability of the I ² or the ratio of IQR squares for the scenario of true ratio of IQR squares = 80.0% (large between-study variation). The I ² from the normal random effects model (cross/solid line), and those of the ratio of IQR squares from the proposed model (black circle/broken line: Box-Cox transformation, black triangle/dotted line: Box-Cox transformation with the sign inversion)

Fig. 6

Posterior and predictive distribution. a Posterior distribution of the overall mean from the normal random effects model (solid line), and of the overall median from the proposed model (broken line: Box-Cox transformation, dotted line: Box-Cox transformation with the sign inversion), b Predictive distribution with 95 percent prediction interval from the normal random effect model (solid line), and those from the proposed model (black circle/broken line: Box-Cox transformation, black triangle/dotted line: Box-Cox transformation with the sign inversion)

Fig. 7

Predictive probability. The normal random effect model (solid line) and the proposed model (broken line: Box-Cox transformation, dotted line: Box-Cox transformation with the sign inversion)