Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 May 25;10(6):577.
doi: 10.3390/ma10060577.

Influence of the Constitutive Model for Shotcrete on the Predicted Structural Behavior of the Shotcrete Shell of a Deep Tunnel

Matthias Neuner  1 , Magdalena Schreter  2 , David Unteregger  3 , Günter Hofstetter  4
Affiliations

Influence of the Constitutive Model for Shotcrete on the Predicted Structural Behavior of the Shotcrete Shell of a Deep Tunnel

Matthias Neuner et al. Materials (Basel). .

Abstract

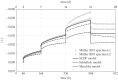
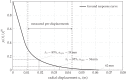
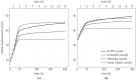
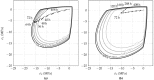
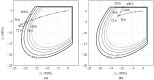
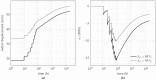
The aim of the present paper is to investigate the influence of the constitutive model for shotcrete on the predicted displacements and stresses in shotcrete shells of deep tunnels. Previously proposed shotcrete models as well as a new extended damage plasticity model for shotcrete are evaluated in the context of 2D finite element simulations of the excavation of a stretch of a deep tunnel by means of the New Austrian Tunneling Method. Thereby, the behavior of the surrounding rock mass is described by the commonly used Hoek-Brown model. Differences in predicted evolutions of displacements and stresses in the shotcrete shell, resulting from the different shotcrete models, are discussed and simulation results are compared to available in situ measurement data.

Keywords: constitutive model; damage model; finite element model; numerical simulation; plasticity model; shotcrete; tunneling.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Schematic view of the benchmark problem together with the 2D axisymmetric finite element model.
Figure 2
Figure 2
Stepwise stress release function pi(t) assumed in the finite element simulations (black curve), which is derived from the idealized parabolic stress release function, proposed by Pöttler [11] (gray curve).
Figure 3
Figure 3
Measured and predicted evolution of the total strain of the two specimens of creep test series No. 4/2 in creep tests on unsealed specimens by Müller [21].
Figure 4
Figure 4
Ground response curve computed on the basis of the Hoek–Brown model.
Figure 5
Figure 5
Comparison of the predicted radial displacement at the shotcrete-rock interface for initial stress release ratios of (a) 85% and (b) 95%.
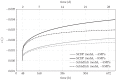
Figure 6
Figure 6
Comparison of the creep behavior, based on the evolution of the total strain, predicted by the SCDP model and the Schädlich model, for sustained compressive stresses of -4 MPa and -8 MPa.
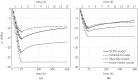
Figure 7
Figure 7
Predicted evolution of the circumferential stress in the shotcrete shell for initial stress release ratios of (a) 85% and (b) 95%.
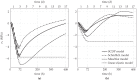
Figure 8
Figure 8
Predicted evolution of the longitudinal stress in the shotcrete shell for initial stress release ratios of (a) 85% and (b) 95%.
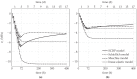
Figure 9
Figure 9
Predicted evolution of the longitudinal stress, if shrinkage of shotcrete is neglected, for initial stress release ratios of (a) 85% and (b) 95%.
Figure 10
Figure 10
Evolution of biaxial strength envelopes of shotcrete and stress paths, predicted by the SCDP model for initial stress release ratios of (a) 85% and (b) 95%.
Figure 11
Figure 11
Evolution of biaxial strength envelopes of shotcrete and stress paths, predicted by the Schädlich model for initial stress release ratios of (a) 85% and (b) 95%.
Figure 12
Figure 12
Evolution of biaxial strength envelopes of shotcrete and stress paths, predicted by the Meschke model for initial stress release ratios of (a) 85% and (b) 95%.
Figure 13
Figure 13
Long-term behavior predicted by the SCDP model for both initial stress release ratios: evolution of (a) the radial displacement and (b) the circumferential stress.
See this image and copyright information in PMC

References

    1. Meschke G. Consideration of aging of shotcrete in the context of a 3D-viscoplastic material model. Int. J. Numer. Methods Eng. 1996;39:3145–3162. doi: 10.1002/(SICI)1097-0207(19960930)39:18<3145::AID-NME992>3.0.CO;2-M. - DOI
    1. Bažant Z., Panula L. Practical prediction of time-dependent deformations of concrete. Mater. Struct. 1978;11:307–328.
    1. Schädlich B., Schweiger H.F. A new constitutive model for shotcrete; Proceedings of the 8th European Conference on Numerical Methods in Geotechnical Engineering; Delft, The Netherlands. 18–20 June 2014; Leiden, The Netherlands: CRC Press Taylor & Francis; 2014. pp. 103–108.
    1. 209R-92: Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures. American Concrete Institute (ACI); Farmington Hills, MI, USA: 1992. ACI Committee 209.
    1. Hellmich C., Ulm F.J., Mang H.A. Multisurface chemoplasticity. I: Material model for shotcrete. J. Eng. Mech. 1999;125:692–701. doi: 10.1061/(ASCE)0733-9399(1999)125:6(692). - DOI

LinkOut - more resources