Learning unbelievable probabilities
Abstract
Loopy belief propagation performs approximate inference on graphical models with loops. One might hope to compensate for the approximation by adjusting model parameters. Learning algorithms for this purpose have been explored previously, and the claim has been made that every set of locally consistent marginals can arise from belief propagation run on a graphical model. On the contrary, here we show that many probability distributions have marginals that cannot be reached by belief propagation using any set of model parameters or any learning algorithm. We call such marginals 'unbelievable.' This problem occurs whenever the Hessian of the Bethe free energy is not positive-definite at the target marginals. All learning algorithms for belief propagation necessarily fail in these cases, producing beliefs or sets of beliefs that may even be worse than the pre-learning approximation. We then show that averaging inaccurate beliefs, each obtained from belief propagation using model parameters perturbed about some learned mean values, can achieve the unbelievable marginals.
Figures
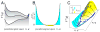
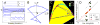

References
-
- Cooper G. The computational complexity of probabilistic inference using bayesian belief networks. Artificial intelligence. 1990;42:393–405.
-
- Pearl J. Probabilistic reasoning in intelligent systems: networks of plausible inference. Morgan Kaufmann Publishers; San Mateo CA: 1988.
-
- Kschischang F, Frey B, Loeliger H. Factor graphs and the sum-product algorithm. IEEE Transactions on Information Theory. 2001;47:498–519.
-
- Bishop C. Pattern recognition and machine learning. Springer; New York: 2006.
-
- Wainwright M, Jordan M. Graphical models, exponential families, and variational inference. Foundations and Trends in Machine Learning. 2008;1:1–305.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
