Quantifying enzyme activity in living cells

Abstract

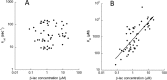
For over a century, enzymatic activity has been studied in vitro, assuming similar activity in the crowded cellular milieu. Here, we determined in real time the catalytic activity of TEM1-β-lactamase inside living cells and compared the values to those obtained in vitro We found the apparent in vivo catalytic efficiency, k_cat/K_m , to be lower than in vitro, with significant cell-to-cell variability. Surprisingly, the results show that inside the cell the apparent catalytic efficiency decreases, and K_m increases with increasing enzyme concentration. To rationalize these findings, we measured enzyme and substrate diffusion rates in the cell and found the latter to be slower than expected. Simulations showed that for attenuated diffusion the substrate flux becomes rate-limiting, explaining why reaction rates in vivo can be independent on enzyme concentrations. The octanol/water partition of the substrate is 4.5, which is in the range of Food and Drug Administration-approved drugs. This suggests substrate-limited reaction rates to be common. These findings indicate that in vitro data cannot be simply extrapolated to the crowded in vivo environment.

Keywords: Michaelis–Menten; beta-lactamase; biophysics; enzyme; enzyme kinetics; in vivo imaging.

Figure 1.

Measuring β-lac induced catalysis in living cells. A, product, mCherry, and transmission channels are shown before and at t = 0, 10, and 60 s after CCF2 injection. The increase in the product channel intensity after injection results from the cleavage of the fluorogenic substrate. A complete animation of the injected cell is shown in supplemental Movie S1. B, product formation and mCherry-β-lac were followed over the course of the experiment, with the curve being the intensity measured within a defined ROI (yellow circle). The red and light blue circles represent cases where multiple ROIs from the same cell were analyzed separately. In this experiment, mCherry-β-lac concentration was 1.2 μm, and the substrate concentration was 10.5 μm according to the calibration curve (supplemental Fig. S1, B and C).

Figure 2.

Catalytic efficiency for β-lac using CCF2 as substrate. k_cat/K_m values were calculated from single progress curves (see supplemental Fig. S2A). Each dot is the value calculated from one progress curve. For live cell measurements, CCF2 was microinjected into the cytoplasm of transfected cells (A, left column, and C). The substrate and enzyme concentrations were calculated from a calibration curve as shown in supplemental Fig. S1, B and C. For cell extract measurements, varying amounts (0.5 to 100 μm) of CCF2 were mixed with cell extract (∼4 mg/ml) containing cytoplasmic (0.03 μm produced in HeLa cells) or the recombinant (0.1 μm produced in E. coli) mCherry-β-lac. The long line in each column indicates the average values calculated from the individual progress curves. The shorter lines and inset in B show the range (average k_cat/K_m ± S.D.) as calculated from fitting [V₀] versus [S] using the M–M equation (see supplemental Fig. S3, A and B). B shows values determined in vitro with CENTA as substrate measured on a stopped flow. C shows in-cell values for the wild-type and for two β-lac mutants: G238S and R244Q.

Figure 3.

Analyzing the variance in apparent catalytic efficiency of β-lac. A, variation in k_cat/K_m between cells in relation to variation between three separately analyzed ROIs within the same cell. B, cell-to-cell variability of k_cat/K_m at three ROIs and between measurements done on different days (days 1–5) of the wild-type β-lac without and in the presence of NaN₃. Each dot represents one cell. C, β-lac concentration versus k_cat/K_m of individual cells. D, V_max/K_m and k_cat/K_m for individual cells. E, determined progress curves for nine cells at [E] ranging from 0.2 to 4.3 μm and [S₀] ranging from 6 to 35 μm. F, the progress curves in E were normalized by [S₀], showing the independence of the reaction on [E].

Figure 4.

β-lac activity in vitro scales with concentration. A, relative β-lac concentrations versus V₀ of individual progress curves recorded using 5–80 nm of β-lac and 50 μm CENTA (T = 27 °C) measured in a stopped flow. The values are averages of three independent measurements. B, k_cat, K_m, and k_cat/K_m values calculated from progression curve fitting of the individual measurements used in A. C, plotting [S₀] versus k_cat/K_m for individual cells shown in Fig. 2C).

Figure 5.

k_cat and K_m values of β-lac in vivo. A, k_cat values from single cell measurements of β-lac and CCF2. The cells are those shown in Fig. 3C, and the analysis was done by single progress curve fitting. B, K_m values of the cells in A.

Figure 6.

FRAP measurements in HeLa cells. A, FRAP measurements of mCherry-β-lac, mCherry, mCherry-β-gal, CCF2, FDG, and RDG. The target area was bleached with maximum intensity (see “Materials and methods”), and time-lapse images were acquired at 1-ms intervals. t_½ were calculated by fitting the recovery to an exponential curve. Differences in FRAP between the different molecules was calculated using analysis of variance and Bonferroni as post hoc. *, p = 0.01–0.05; **, p = 0.001–0.01; ***, p < 0.001. B, fraction recovery after FRAP was determined as the fluorescence at 1.4 s divided by that before FRAP.

SCHEME 1

Figure 7.

Simulating progress curves of β-lac. A, simulating individual progress curves using Scheme 1 with [S₀] and [E] being the same as the experimental curves in Fig. 3E. For the simulation k₁ and k₋₁ were 0.05 s⁻¹, k₂ was 10 s⁻¹, k₋₂ was 600 s⁻¹, and k_cat was 55 s⁻¹. B, normalizing the curves in A by [S₀] (as done in Fig. 3F) results in overlay of the simulated reaction curves. C, simulating individual progress curves with [E] being attenuated by [X]. D, the data in C were normalized by [S₀] (as done in Fig. 3F). E, simulating individual progress curves without any attenuation. F, the data in E were normalized by [S₀]. The simulations were done using ProKII (Applied Photosystems).

Figure 8.

Simulating reaction progress curves using 0.5 and 5 μm enzyme. Simulating progress curves according to Scheme 1 where [SX₀] = 30 μm, [E] = 0.5 and 5 μm, k₁ and k₋₁ = 0.05 s⁻¹, k₂ = 10 s⁻¹, k₋₂ = 600 s⁻¹, and k_cat = 55 s⁻¹. The simulations were done using ProKII (Applied Photosystems).