Fragmentation in spin ice from magnetic charge injection

Abstract

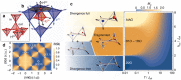
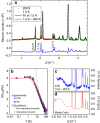
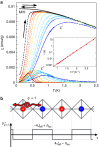
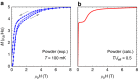
The complexity embedded in condensed matter fertilizes the discovery of new states of matter, enriched by ingredients like frustration. Illustrating examples in magnetic systems are Kitaev spin liquids, skyrmions phases, or spin ices. These unconventional ground states support exotic excitations, for example the magnetic charges in spin ices, also called monopoles. Here, we propose a mechanism to inject monopoles in a spin ice at equilibrium through a staggered magnetic field. We show theoretically, and demonstrate experimentally in the Ho₂Ir₂O₇ pyrochlore iridate, that it results in the stabilization of a monopole crystal, which exhibits magnetic fragmentation. In this new state of matter, the magnetic moment fragments into an ordered part and a persistently fluctuating one. Compared to conventional spin ices, the different nature of the excitations in this fragmented state opens the way to tunable field-induced and dynamical behaviors.Exploring unconventional magnetism facilities both fundamental understanding of materials and their real applications. Here the authors demonstrate that a magnetic monopole crystal is stabilized by a staggered magnetic field in the pyrochlore iridate Ho₂Ir₂O₇, leading to a fragmented magnetization.

Fig. 1

Staggered field in a pyrochlore lattice and magnetic fragmentation. a Pyrochlore lattice submitted to 〈111〉 staggered field represented by the arrows on each site, with in and out tetrahedra when this field points either inward or outward of the tetrahedra. b Structure of the pyrochlore iridate Ho₂Ir₂O₇ with the Ho³⁺ ions (red) and the Ir⁴⁺ ions (blue), both occupying a pyrochlore lattice. Each rare-earth is surrounded by a hexagon of six Ir nearest neighbors. When the iridium lattice orders magnetically in the AIAO phase, as shown on the blue lattice, a local magnetic field, perpendicular to the hexagon plane, hence aligned along the local 〈111〉 directions, is felt by the central rare-earth ion, as represented in a. c Phase diagram as a function of reduced temperature $T\mathrm{∕}{\mathcal{J}}_{\mathrm{eff}}$ and local field $h_{\mathrm{loc}}\mathrm{∕}{\mathcal{J}}_{\mathrm{eff}}$, defined through the charge order parameter $M_q=⟨∣\frac{1}{N}{\sum }_{\alpha =1}^N{\Delta }_{\alpha }{q}_{\alpha }∣⟩$where N is the number of tetrahedra and Δ _α = +1 (−1) for in (out) tetrahedra carrying a charge q _α. As $h_{\mathrm{loc}}\mathrm{∕}{\mathcal{J}}_{\mathrm{eff}}$ increases, the ground state changes from the spin ice (M _q = 0, blue), to the AIAO state (M _q = 2, yellow), going through the charge crystal intermediate phase which fragments (M _q = 1, orange). The fragmentation can be described by the splitting of the pseudo-spin σ = ±1: the divergence free fragment on a tetrahedron can then be written as a state with four spins such that ${\sigma }_{⟨∣q∣⟩=0}$ = (±1/2, ±1/2, ±1/2, and ∓3/2), while the divergence full fragment that carries the magnetic charge corresponds to an AIAO configuration with half of the moment so that ${\sigma }_{⟨∣q∣⟩=1}$ = (±1/2, ±1/2, ±1/2, ±1/2). All the spin and charge configurations are shown in the left panel of c at T = 0. d Magnetic scattering function S(Q), with Q the scattering vector, calculated in the fragmented phase. It shows a diffuse pattern with pinch points (evidenced by arrows) together with the magnetic Bragg peaks (highlighted by circles) characteristic of the AIAO ordered state, but whose intensity (proportional to the magnetic moment squared) is a quarter of that expected when the whole magnetic moment is ordered

Fig. 2

Magnetic ordering and diffuse scattering in Ho₂Ir₂O₇. a Neutron diffractograms recorded at 200 K (red dots) and 1.5 K (green dots) showing the rise of magnetic Bragg peaks. The 1.5 K Rietveld refinement (black line) using a k = 0 propagation vector yields an AIAO magnetic order for the holmium sublattice. The difference between the 1.5 and 200 K data (blue line, shifted for clarity) enhances the magnetic Bragg peaks. b Temperature evolution of the refined Ho³⁺ magnetic moment, in a semi-logarithmic scale, measured with two diffractometers (D1B and G4.1). The red dashed curve is the calculated ordered magnetic moment induced by the temperature dependent molecular field created by the Ir magnetic ordering. Below 20 K, the calculated and experimental curves depart from each other due to the presence of Ho-Ho magnetic interactions. The red full curve is obtained from Monte Carlo calculations (Eq. (1)) with ${\mathcal{J}}_{\mathrm{eff}}$ = 1.4 K and h _loc/${\mathcal{J}}_{\mathrm{eff}}$ = 4.5, the colored area representing the calculated values compatible with the experimental error bars (within symbol size). These calculations allow to account for the saturation of the ordered moment below 2 K due to fragmentation. The departure above 40 K between the calculated and experimental curves is attributed to the decrease of the Ir molecular field. c Evidence for diffuse scattering at 1.5 K, from the difference between the 1.5 and 200 K diffractograms (the negative intensity is due to an imperfect subtraction of a strong nuclear peak caused by the lattice parameter variation). d Powder average magnetic scattering function S(Q) from Monte Carlo calculations at T/${\mathcal{J}}_{\mathrm{eff}}$ = 0.05 with h _loc/${\mathcal{J}}_{\mathrm{eff}}$ = 4.5

Fig. 3

Dynamical properties and diffusion of the excitations. a Low temperature dependence of the ZFC-FC magnetization performed in 5 mT below 4 K (black symbols). The two curves depart below about 1.5 K. On the same graph are shown the real part χ′ and imaginary part χ″ of the AC susceptibility vs T at several frequencies f from 0.011 Hz (red) to 570 Hz (blue) with the intermediate frequencies 0.057, 0.21, 1.11, 5.7, 21, 57 and 111 Hz. Inset: τ vs 1/T, where τ = 1/2πf _peak and f _peak is the maximum of χ″(f) measured at constant temperature T. The line is a fit to an Arrhenius law τ = τ ₀exp(E/T) where τ ₀ = (1.2 ± 0.2) × 10⁻⁵ s and E = 4.8 ± 0.1 K. b Two-dimensional representation of a string of tetrahedra on which an elementary excitation carrying a charge q = +1 (red disc with black border) diffuses in the fragmented regime Spatial periodic potential $V_q^{\alpha }$ felt by the diffusing charge and induced by the underlying static charge crystal, where α refers to the tetrahedron type: α = in carries an ordered charge $q_o^{\mathrm{in}}=+1$ (red) and α = out carries $q_o^{\mathrm{out}}=-1$ (blue)

Fig. 4

Magnetization, measurements and calculations. a M vs H measured at 110 mK. The empty symbols show the first magnetization curve and the filled symbols the magnetization curves obtained afterwards by ramping the field up and down. The small hysteresis opening is due to the existence of slow dynamics at low temperature. b Calculated M vs H for h _loc/${\mathcal{J}}_{\mathrm{eff}}$ = 4.5 and T/${\mathcal{J}}_{\mathrm{eff}}$ = 0.5, performing a powder averaging. The anomalies, mimicking the experimental curve, feature the existence of an exotic field-induced behavior exhibiting magnetization plateaus