Unzipping Zipf's law

Abstract

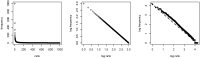
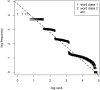
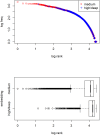
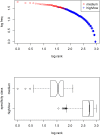
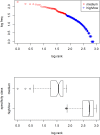
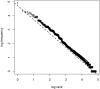
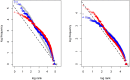
In spite of decades of theorizing, the origins of Zipf's law remain elusive. I propose that a Zipfian distribution straightforwardly follows from the interaction of syntax (word classes differing in class size) and semantics (words having to be sufficiently specific to be distinctive and sufficiently general to be reusable). These factors are independently motivated and well-established ingredients of a natural-language system. Using a computational model, it is shown that neither of these ingredients suffices to produce a Zipfian distribution on its own and that the results deviate from the Zipfian ideal only in the same way as natural language itself does.

Fig 1. Zipf’s law.

A: Predicted frequency by rank. B: Predicted frequency by rank in double-log space. C: Frequency development in Melville’s Moby Dick.

Fig 2. Attempt to generate a Zipfian distribution with syntax only.

To generate these results, the class frequencies and class sizes reported for Dutch in Table 1 are used. Numbers correspond to word classes when ordered by expected frequency.

Fig 3. Frequency distributions of different specifity classes in the Brown corpus.

Top panel: distribution over overall distribution of nouns. Degree of meaning specification is approximated by automatically determining the depth of embedding in the WordNet noun taxonomy. Words with lowest ranks are all moderately specified with an embedding of 3–9 (red circles). Bottom panel: boxplots of frequency ranks per specificity class.

Fig 4. Frequency distribution of different specificity classes in a computer simulation.

The lexicon consists of 1,000 words with ten optional meaning dimensions, from which words are selected for 10,000 contexts with randomly generated targets and 5 randomly generated distractors. Words with lowest ranks are all moderately specified (2–4 dimensions; red circles). Bottom panel: boxplots of frequency ranks per specificity class.

Fig 5. Distribution of probability of usage of different specificity classes in a computational model.

The lexicon consists of 1,000 words with ten optional meaning dimensions. Probability of usage depends on degree of specification and number of distractors assumed (here 5). As in the previous figures, words with lowest ranks are all moderately specified (3–6 dimensions; red circles). Bottom panel: boxplots of frequency ranks per specificity class.

Fig 6. Generating Zipf’s law by combining syntax and semantics.

10 word classes of equal frequency are used with 5, 30, 50, 100, 500, 500, 1,000, 15,000, 25,000, and 100,000 members; items can be specified for maximally 30 meaning dimensions (mean 8.3, sd 2.0), and the number of distractors is 5.

Fig 7. Frequency distribution in CGN (left) and Brown corpus (right).

Blue triangles show the results of the model simulation using the corresponding parameters from Table 1; red plusses show the results when mixing the CGN and Brown parameters.