Impact of interaction style and degree on the evolution of cooperation on Barabási-Albert scale-free network

Abstract

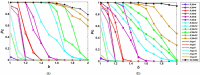
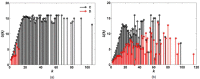
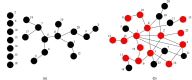
In this work, we study an evolutionary prisoner's dilemma game (PDG) on Barabási-Albert scale-free networks with limited player interactions, and explore the effect of interaction style and degree on cooperation. The results show that high-degree preference interaction, namely the most applicable interaction in the real world, is less beneficial for emergence of cooperation on scale-free networks than random interaction. Besides, cooperation on scale-free networks is enhanced with the increase of interaction degree regardless whether the interaction is high-degree preference or random. If the interaction degree is very low, the cooperation level on scale-free networks is much lower than that on regular ring networks, which is against the common belief that scale-free networks must be more beneficial for cooperation. Our analysis indicates that the interaction relations, the strategy and the game payoff of high-connectivity players play important roles in the evolution of cooperation on scale-free networks. A certain number of interactions are necessary for scale-free networks to exhibit strong capability of facilitating cooperation. Our work provides important insight for members on how to interact with others in a social organization.

Fig 1. The interacting process of players.

Fig 2

Density of cooperators P_C on scale-free networks as a function of defection temptation b for different upper-bounds W under population size (a) N = 1000 and (b) N = 10000. R and H correspond to random interaction and high-degree interaction, respectively. The result on corresponding regular ring-W networks is denoted by the dotted line with the same color.

Fig 3. Density of cooperators P_C on scale-free networks as a function of defection temptation b for different upper-bounds W under a standard PDG parameter combination R = 1, P = 0, S = −0.1,2.1 > b > 1.

Population size is set as N = 1000. R and H correspond to random interaction and high-degree interaction, respectively. The result on corresponding regular ring-W networks is denoted by the dotted line with the same color.

Fig 4

Average payoff U(k) of a player of degree k in the stationary regime of evolutionary dynamics under (a) random interaction and (b) high-degree preference interaction. Cooperator is denoted by C with black and defector by D with red. Defect temptation and upper-bound are set to b = 1.7 and W = 16, respectively.

Fig 5

Interaction relation networks formed by all players in the stationary regime of evolutionary dynamics under (a) random interaction and (b) high-degree preference interaction. Defect temptation and upper-bound are set to b = 1.7 and W = 16, respectively.

Fig 6

Interaction relations among high-connectivity players and their strategies in the stationary regime of evolutionary dynamics under (a) random interaction and (b) high-degree preference interaction. Defect temptation and upper-bound are set to b = 1.7 and W = 16, respectively. Cooperator is denoted with black node and defector with red node.

Fig 7

Frequency of the cooperative interacting-neighbors of high-connectivity players under (a) random interaction and (b) high-degree preference interaction. Cooperator is denoted by C with black and defector by D with red.

Fig 8

Average payoff U(k) of a player of degree k in the stationary regime of evolutionary dynamics under (a) W = 4, b = 1.01, (b) W = 6, b = 1.2 and (c) W = 8, b = 1.3. Cooperator is denoted by C with black and defector by D with red.

Fig 9. Interaction relations among all cooperators in the stationary regime of evolutionary dynamics under upper-bound W = 4.

Defect temptation is set to b = 1.01.

Fig 10. Probability P_C(k) of a player of degree k playing as a cooperator in the stationary regime of evolutionary dynamics.

The random selection rule is applied and l = 20.