Foldamer hypothesis for the growth and sequence differentiation of prebiotic polymers
- PMID: 28831002
- PMCID: PMC5594640
- DOI: 10.1073/pnas.1620179114
Foldamer hypothesis for the growth and sequence differentiation of prebiotic polymers
Abstract
It is not known how life originated. It is thought that prebiotic processes were able to synthesize short random polymers. However, then, how do short-chain molecules spontaneously grow longer? Also, how would random chains grow more informational and become autocatalytic (i.e., increasing their own concentrations)? We study the folding and binding of random sequences of hydrophobic ([Formula: see text]) and polar ([Formula: see text]) monomers in a computational model. We find that even short hydrophobic polar (HP) chains can collapse into relatively compact structures, exposing hydrophobic surfaces. In this way, they act as primitive versions of today's protein catalysts, elongating other such HP polymers as ribosomes would now do. Such foldamer catalysts are shown to form an autocatalytic set, through which short chains grow into longer chains that have particular sequences. An attractive feature of this model is that it does not overconverge to a single solution; it gives ensembles that could further evolve under selection. This mechanism describes how specific sequences and conformations could contribute to the chemistry-to-biology (CTB) transition.
Keywords: HP model; autocatalytic sets; biopolymers; origin of life.
Conflict of interest statement
The authors declare no conflict of interest.
Figures





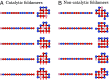
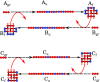
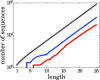

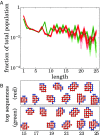
References
-
- Joyce G. Nonenzymatic template-directed synthesis of informational macromolecules. Cold Spring Harb Symp Quant Biol. 1987;52:41–51. - PubMed
-
- Eigen M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften. 1971;58:465–523. - PubMed
-
- Eigen M, Schuster P. A principle of natural self-organization. Naturwissenschaften. 1977;64:541–565. - PubMed
-
- Eigen M, Schuster P. The hypercycle. Naturwissenschaften. 1978;65:7–41. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous

