Maximum entropy models capture melodic styles
- PMID: 28835642
- PMCID: PMC5569059
- DOI: 10.1038/s41598-017-08028-4
Maximum entropy models capture melodic styles
Abstract
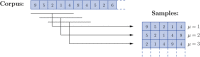
We introduce a Maximum Entropy model able to capture the statistics of melodies in music. The model can be used to generate new melodies that emulate the style of a given musical corpus. Instead of using the n-body interactions of (n-1)-order Markov models, traditionally used in automatic music generation, we use a k-nearest neighbour model with pairwise interactions only. In that way, we keep the number of parameters low and avoid over-fitting problems typical of Markov models. We show that long-range musical phrases don't need to be explicitly enforced using high-order Markov interactions, but can instead emerge from multiple, competing, pairwise interactions. We validate our Maximum Entropy model by contrasting how much the generated sequences capture the style of the original corpus without plagiarizing it. To this end we use a data-compression approach to discriminate the levels of borrowing and innovation featured by the artificial sequences. Our modelling scheme outperforms both fixed-order and variable-order Markov models. This shows that, despite being based only on pairwise interactions, our scheme opens the possibility to generate musically sensible alterations of the original phrases, providing a way to generate innovation.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures

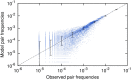
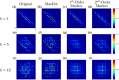
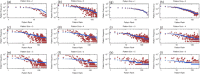
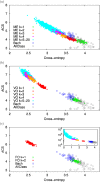
References
-
- Bialek, W. & Ranganathan, R. Rediscovering the power of pairwise interactions. arXiv preprint arXiv:0712.4397 (2007).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

