A Comparison of Agent-Based Models and the Parametric G-Formula for Causal Inference

Abstract

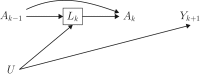
Decision-making requires choosing from treatments on the basis of correctly estimated outcome distributions under each treatment. In the absence of randomized trials, 2 possible approaches are the parametric g-formula and agent-based models (ABMs). The g-formula has been used exclusively to estimate effects in the population from which data were collected, whereas ABMs are commonly used to estimate effects in multiple populations, necessitating stronger assumptions. Here, we describe potential biases that arise when ABM assumptions do not hold. To do so, we estimated 12-month mortality risk in simulated populations differing in prevalence of an unknown common cause of mortality and a time-varying confounder. The ABM and g-formula correctly estimated mortality and causal effects when all inputs were from the target population. However, whenever any inputs came from another population, the ABM gave biased estimates of mortality-and often of causal effects even when the true effect was null. In the absence of unmeasured confounding and model misspecification, both methods produce valid causal inferences for a given population when all inputs are from that population. However, ABMs may result in bias when extrapolated to populations that differ on the distribution of unmeasured outcome determinants, even when the causal network linking variables is identical.

Keywords: Monte Carlo methods; agent-based models; causal inference; decision analysis; individual-level models; mathematical models; medical decision making; parametric g-formula.

Figure 1.

Simplified decision process for the use of treatment among HIV-positive individuals at each month k. Square black nodes represent decision points where intervention is possible, white circles represent nodes where an individual's path depends on the conditional probability distribution specified, and triangles represent terminal nodes.

Figure 2.

Causal directed acyclic graph depicting 2 arbitrary time points from a setting with a time-varying treatment A that has no causal effect on the outcome Y. Conventional adjustment for the confounder L by regression or stratification is expected to introduce bias, because L is affected by prior treatment and shares a cause (U) with the outcome.